「流動性の罠 再考」で示したようにマネタリーベースの増加が期待物価上昇率に影響する経路はあるのでしょうか。消費者物価(CPI)の過去20年間のデータに注目すると、ドル円為替レートと連動して推移しているのがわかります。金融緩和が日米の金利差の変動をドル円為替レートに反映して、間接的にCPIに影響にする経路はあります。CPIとドル円為替レートの関係を分析してモデルを構築してみます。
CPI - USDJPY為替レートの因果関係
日本の食料自給率はおよそ4割です。主食の米以外の多くの食品が輸入されています。国際的な貿易取引量(注1)は拡大して、その他の消費財についても輸入品の占める割合は多くなってきています。このことからCPIと外国為替レートには因果関係があることが推測されます。二つの指標の過去20年の時系列データを用いて両者の因果関係について調べてみます。
CPIとUSDJPY為替レート、二つの時系列データに関してGranger因果律(注2)を計算します。二つの時系列データの因果律はベクター自己回帰 (Vector Auto Regression:VAR)モデルを適用して、帰無仮説が棄却できるかどうかで因果性を識別できます。Granger因果律を計算し、帰無仮説が棄却できない場合、両者には因果関係がないとみなせます。
(注2):Granger 因果性
以下のベクター自己回帰モデルを考えます。
Xt = c + Σαi Xt-l + Σ βj Yt-j + εt
Yt = c' + Σα'i Yt-l + Σ β'j Xt-j + ηt
εt、ηt:ホワイトノイズ{Yt} が{Xt}のGranger因果性がない場合、全てのj=1,2,....Lyについて、帰無仮説
H0: β1 = β2 = .... = βLy = 0H0: Yt -\-> Xt
が成立します。
因果推定で、p値が0.05より大きい場合、帰無仮説が棄却できないため、Yt は Xt のGranger因果性はないとみなします。
CPIと外国為替レートの関係についてGranger因果性を推定します。CPIのデータは総務省が公表しているWebサイト等から取得できます。USDJPY為替レートは民間の金融機関やデータ提供サイトから取得可能です。二つの時系列データは2002年01月〜2023年11月までの月次データを用います。
以下のデータ系列を使用します。
図1 CPI , USDJPY為替レートのデータ系列
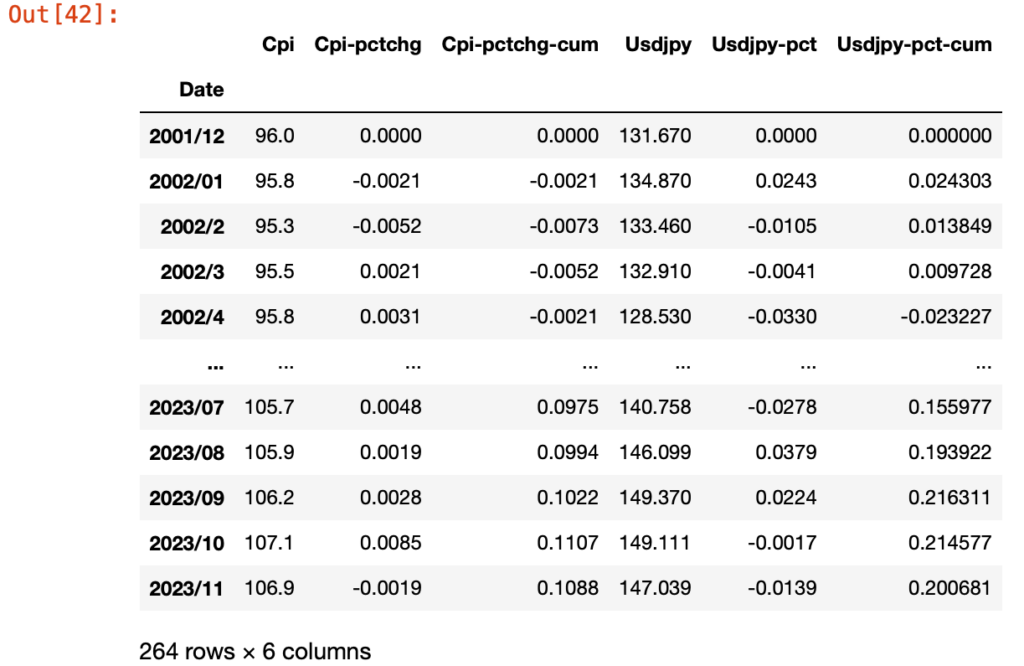
Granger因果律のp-値が0.05より大きい場合に帰無仮説が棄却できないとみなします。帰無仮説が棄却できない場合、二つの時系列データ間での因果性は認められません。つまりCPIと為替レートの時系列な変動に因果関係はありません。
計算にはVARモデルを使用します。上の図で示したcsv形式のデータをpythonのpandasデータフレームに読み込んで、モデルのAPIの引数のnumpy形式に変換します。以下モデルの構築と検証のソースコードはpython で作成します。
df_x = pd.read_csv(ファイルのパス,index_col=0)
df = pd.DataFrame({'x':df_x['Cpi-pctchg-cum'],'y':df_x['Usdjpy-pct-cum']})
# データフレームを配列へ変換
data = df.to_numpy()最大ラグを10(10ヶ月)に設定し、AICを用いて最適なラグを探索します。計算結果を示します。
図2 VARモデルの計算結果
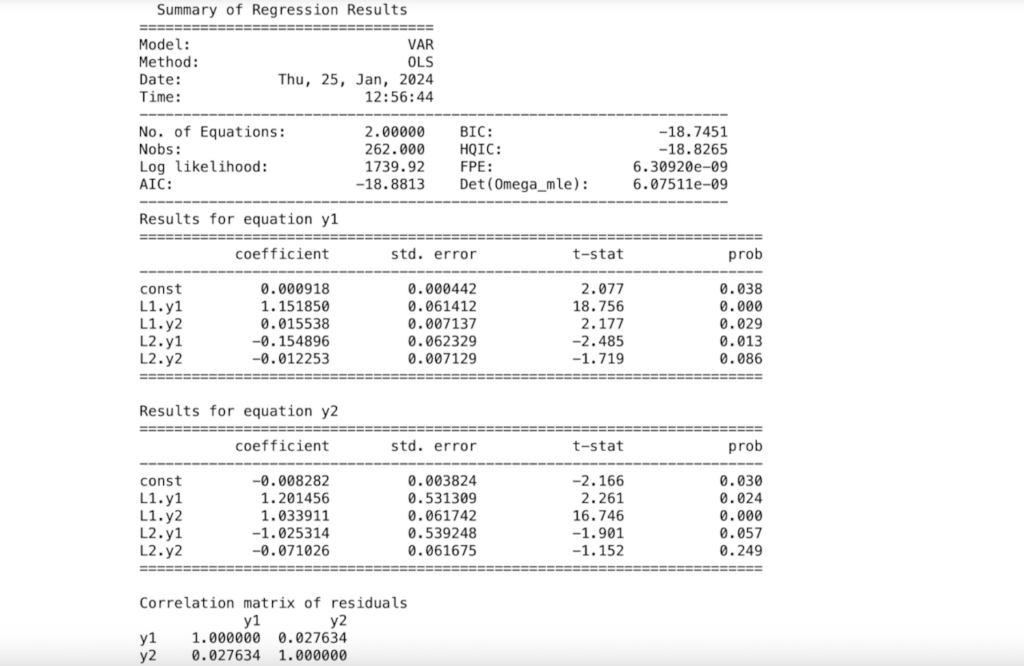
該当期間についてp-値を計算してみると、p-値は0.008413083698398213、つまり0.05以下となり帰無仮説が棄却できました。

この期間のCPIと為替レートの間に明確な因果関係があるとみなせます。
因果性 スキャッターと密度の図示
二つの指標の時系列データの依存性を調べるために、pythonの因果推論のライブラリtigramiteを使ってみます。Granger因果律の計算に用いた図1のデータの系列を用います。
因果推論に必要なパッケージをインポートします。
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.parcorr_wls import ParCorrWLS
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.independence_tests.gsquared import Gsquared
from tigramite.independence_tests.regressionCI import RegressionCI
データを図示してみましょう。
var_names = [r'$CPI$', r'$USD-JPY$']
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()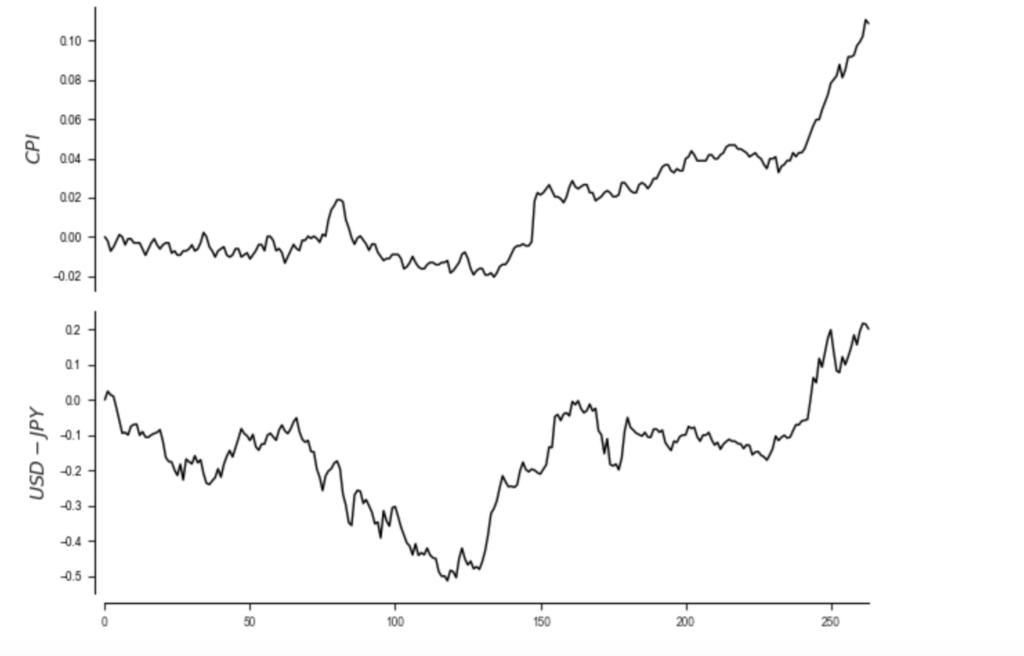
図3 CPI、USD-JPY為替レートの推移 (2002年1月ー2023年11月)
CPIとUSDJPY為替レートの間の依存性を調べるために、従属性が線形であるかどうかをみてみます。スキャッタープロットと密度プロットを使います。
matrix_lags = None #np.argmax(np.abs(correlations), axis=2)
tp.plot_scatterplots(dataframe=dataframe, add_scatterplot_args={'matrix_lags':matrix_lags}); plt.show()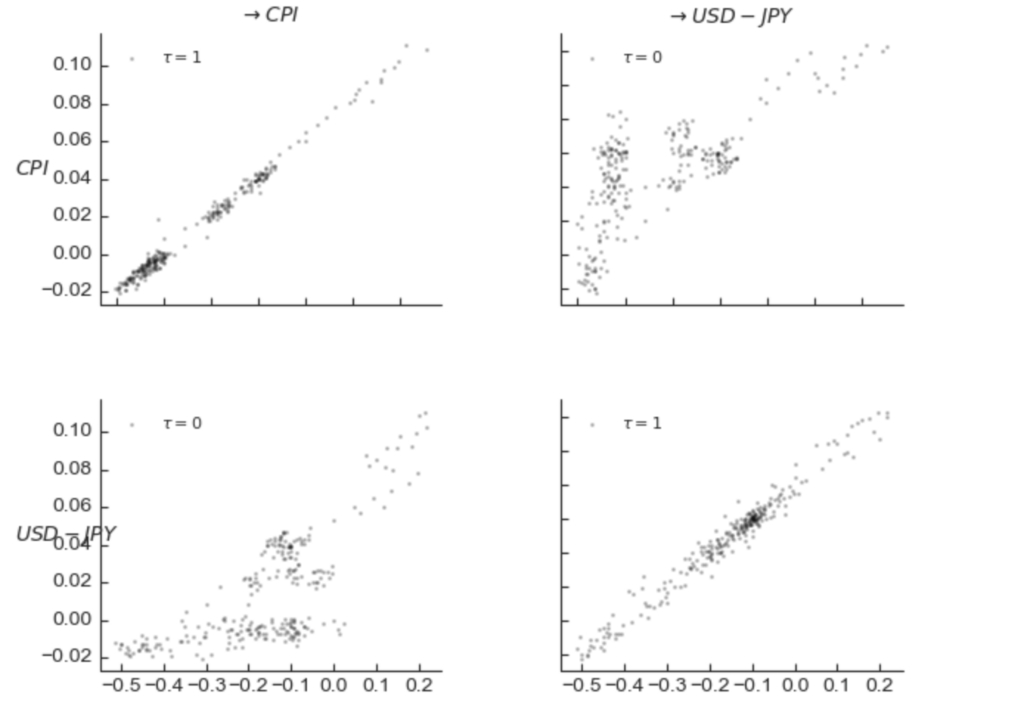
図4 CPI, USD-JPY為替レートのスキャッタープロット
密度を表示します。
tp.plot_densityplots(dataframe=dataframe, add_densityplot_args={'matrix_lags':matrix_lags})
plt.show()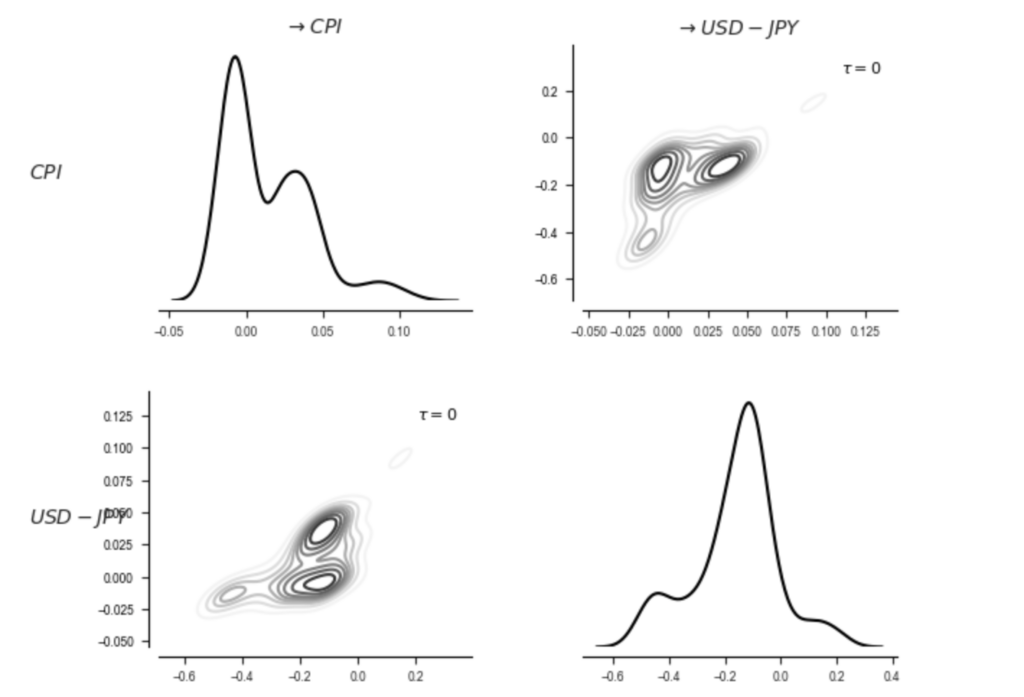
図5 CPI、USD-JPY為替レートの密度
CPI-為替レートモデル
上で図示したように、両者には線形的な因果関係があることを前提にCPIのモデルを作ります。
Grangerテストによって該当期間に二つの時系列データに因果関係があるとみなせるので、USDJPY為替レートの変動からCPIの値を導出するモデルが作れます。
CPI = f ( x )
x:USDJPY為替レート簡単な線形モデルであれば、
CPI = α x + η
x: USDJPY為替レート、η:ランダムノイズこのモデルを使ってCPIの確率分布を求めることができます。モンテカルロシミュレーションを用いてUSDJPY為替レートの推移データからCPIの事後分布を導出します。
ベイジアン線形回帰モデルで予測したら、どうなるかみてみましょう。pymcを使って回帰モデルを作ります。
最初にpymcのライブラリをインポートします。
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
import pytensor.tensor as pt
import xarray as xrAPIに渡す引数の形式にデータを変換します。
x_out = df['y'].to_numpy()
y_out = df['x'].to_numpy()モデルを定義してサンプラーを動かします。
with pm.Model() as model:
xdata = pm.ConstantData("x", x_out, dims="obs_id")
# 事前分布の定義
intercept = pm.Normal("intercept", mu=0, sigma=1)
alpha = pm.Normal("slope", mu=0, sigma=1)
sigma = pm.HalfCauchy("sigma", beta=10)
mu = pm.Deterministic("mu", intercept + alpha * xdata, dims="obs_id")
# 尤度
likelihood = pm.Normal("y", mu=mu, sigma=sigma, observed=y_out, dims="obs_id")
# 推定
trace = pm.sample(tune=2000)
サンプリングが終了しました。
以下のコードは、事後分布から回帰パラメータを得ることによって事後予測線形線を計算し、それら20の回帰線を図示します。
az.style.use("arviz-darkgrid")
post = az.extract(trace, num_samples=20)
x_plot = xr.DataArray(np.linspace(x_out.min(), x_out.max(), 100), dims="plot_id")
lines = post["intercept"] + post["slope"] * x_plot
plt.scatter(x_out, y_out, label="data")
plt.plot(x_plot, lines.transpose(), alpha=0.4, color="C1")
plt.legend(loc=0)
plt.title("Posterior predictive for normal likelihood");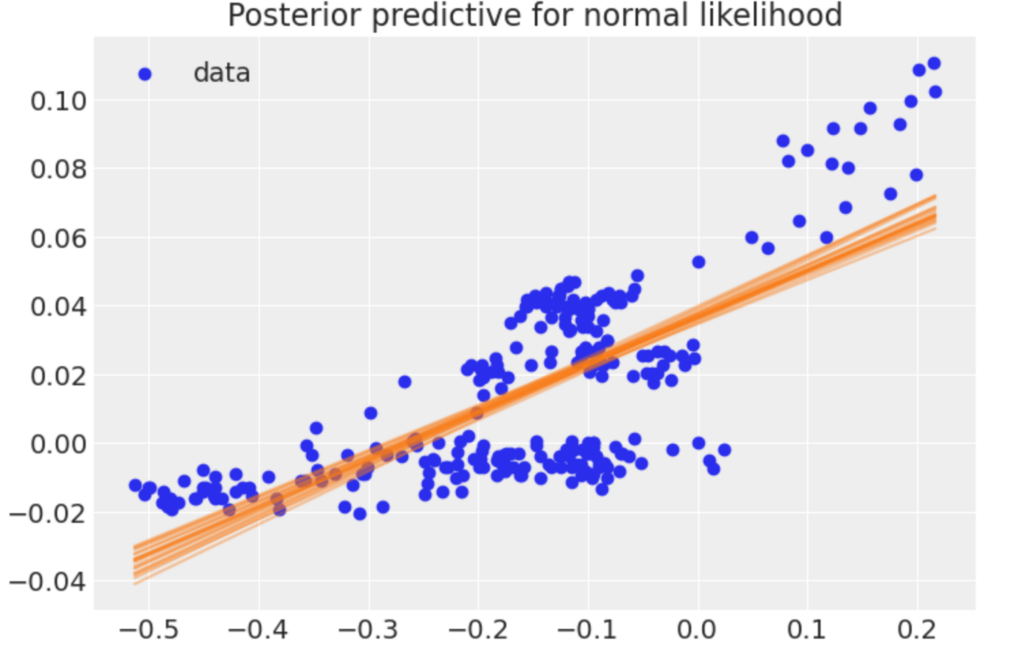
図6 モデルの事後予測
az.plot_trace(trace, var_names=["slope","sigma", "intercept"]);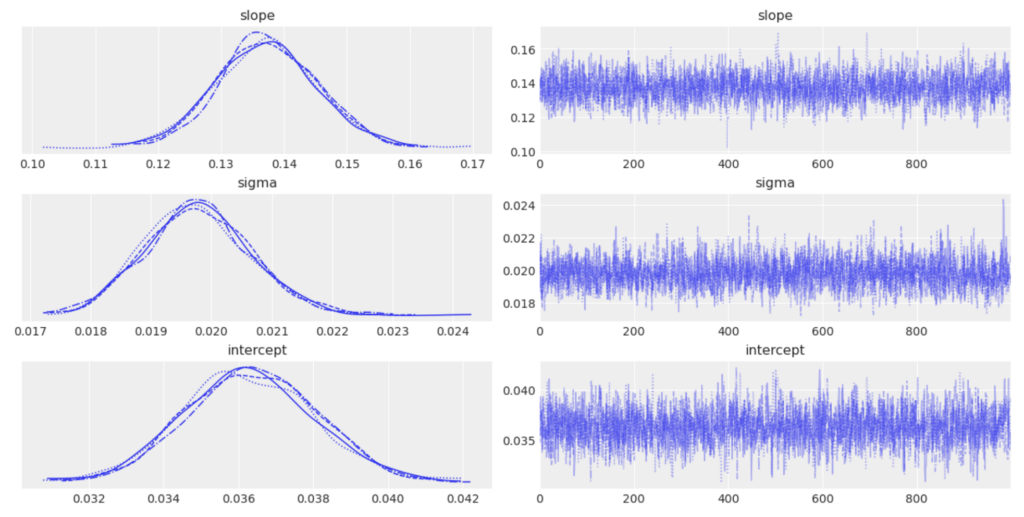
マネタリーベースの増加との関係
このモデルでは、外国為替レートが変動すれば、それに応じて線形的にCPIが変動します。
マネタリーベースの残高の増減との関係では、間接的に外国為替レートを経由して潜在変数である期待物価上昇率とCPIに影響を与えることができます。金融緩和が日米の金利差を生み、USDJPY為替レートに影響します。金利差がUSDJPY為替レートに影響するというモデルをCPIモデルとは別に作ります。
Pearlのintervantionの概念(注3)を反映したモデルでは do(r:r=金利差)を使い、金融緩和のinterventionによる外国為替レートの分布はp(y| do(r=R_DIFF))
政策金利の金利差を変数r=R_DIFFに強制し、外国為替レートに影響を与えます。外国為替レートは市場が決めるのが原則です。本来、外国為替レートに影響を与えるために政策金利を変えることは許容されませんが、金利差は外国為替レートに影響を与えるため、便宜上"rに強制してR_DIFFを与える"という表現を用います。
これによってマネタリーベースの増加は、間接的に外国為替レートを経由してCPIに影響を与えることになります。
ベイジアン階層モデルにPearlのdo-operatorを用いて、P(Y|do(r:r=R_DIFF))を導入し、外国為替レートの変動要因をパラメータ化することはできますが、ここでは単純化したCPIモデルの例を挙げています。
(注3)Judea Pearlは条件確率に対してinterventionとdo-calculusの概念を導入しました。観測値として条件を評価するのでなく、強制的にxに条件Xを与えます。Pearlの因果推論については以下の著作を参照してください。
"Causality Models,Reasoning, and Inference" Judea Pearl
現況と物価動向の予測
ここで日本が直面しているのが、金利はゼロ以下には下げられないという問題です。
日本ではマイナス金利が導入され、0以下で若干の政策余地がありますが、マイナス数%~10%に下げられるわけではありません。
日本の金利はほぼゼロで一定なので、日米の金利差が変動するのはFRBの政策金利に依存するということになります。金利差が外国為替レートに影響するモデルでは、日本の金利が0以下に下げられないため、FRBの政策金利の増減で金利差が変わります。
2022年以後、FRBはインフレ抑制のために金融引き締めを実施し日米の金利差は拡大していました。これはUSDJPY為替レートを円安方向にシフトさせました。これがCPIに反映して目に見える形で物価を上昇させる要因の一つとみなせます。
このモデルでは日本のマネタリーベースの増加は日米金利差に影響しないため、円相場の対ドル為替レートに反映しません。そのためCPIには影響しないことになります。
今後、インフレーションの抑制に成功したFRBが政策金利を下げてくると金利差は縮小し、USDJPYの為替取引のマネーフローは円高方向に逆転します。もちろん金利差だけでなく、地政学的な紛争も外国為替レートや財の価格に反映します。このモデルはそうした地政学的なリスクを考慮に入れていません。ランダムなノイズの項は組み入れてありますが、政治経済的にファットテイルな出来事も発生します。
このモデルは2002年以後の20年間のドル円為替レートとCPIのデータをもとにしています。モデルは現実の近似ですが、ここで検討した外国為替レートだけに依存したCPIのモデルでは、この円の対ドルレートの上昇局面でCPIが再び0近辺から一定水準かそれ以下で推移することを示しています。