極値理論
金融市場に関して、経験的に観測された事実として、価格の収益率のような時系列データの多くに該当する事項があります。
例えば、極端な収益率の値はクラスタを形成するようなことです。
収益率系列における極値は、同期してボラティリティ・クラスタを形成しやすいというようなことです。
極値理論は最大観測値に対するモデルであり、こうした金融時系列データが示す特徴的な現象を記述する上で整合性があります。
株価が急変するような場合、極端な観測値を効率的に使用する点で、株式、株価指数、ポートフォリオの損失に対するモデルとして実際に応用できるでしょう。
閾値モデル
ブロック最大値法
nブロック最大値Mnの分布はnが大きければ、3パラメータGEV分布で近似できます。
GEVとは(Generalized Extreme Value) distribution 一般化極値分布
以下のモデル
G(z) = exp{ -1 [1 + ξ((z - μ)/ σ) ]}
GEVの三つのパラメータは
μ:位置
σ:スケール
ξ:シェイプ xi 形状パラメータ
xi->0 の極限ではグンベル分布になります。
以下の機械学習を実行すると、このパラメータはそれぞれ以下の推定値になります。
xi : 0.155542
sigma: 1.041265
mu: 2.443496
パッケージevirを用います。
evir はExtrem Value in R の略です。
evir
これはS-PLUSのパッケージEVISからRに移植されています。
package evir
バージョン1.7-4
以下のCRANのWebサイトからAPIのマニュアルを参照することができます。
library('evir')
data(danish)
SieLos <-100.0 * siemens
GEV <- gev(SieLos, block="semester")
> library('evir')
次のパッケージを付け加えます: ‘evir’
以下のオブジェクトは ‘package:ggplot2’ からマスクされています:
qplot
> data(siemens)
> SieLos <- 100.0 * simens
エラー: オブジェクト 'simens' がありません
> SieLos <- 100.0 * siemens
> SieGEV <- gev(SieLos, block="semester")
> SieGEV
$n.all
[1] 6146
$n
[1] 48
$data
[1] 3.332837 4.564551 2.929195 3.195160 3.074342 2.847947 2.317558 1.607382
[9] 2.744829 1.353201 1.529342 1.645970 1.730462 1.859042 2.557895 1.772810
[17] 1.489706 2.946031 2.232120 2.157249 3.500081 3.812336 4.518762 3.425502
[25] 3.772542 4.385188 6.070131 4.355276 4.037816 5.117573 7.295798 3.131371
[33] 3.797925 5.732228 2.836112 6.211146 7.672870 3.368053 1.904819 3.829483
[41] 1.809127 3.817076 1.941525 3.345885 1.900642 1.844945 1.934538 1.125012
$block
[1] "semester"
$par.ests
xi sigma mu
0.155542 1.041265 2.443496
$par.ses
xi sigma mu
0.1564440 0.1439107 0.1807022
$varcov
[,1] [,2] [,3]
[1,] 0.024474739 -0.007558325 -0.01260267
[2,] -0.007558325 0.020710290 0.01538971
[3,] -0.012602670 0.015389708 0.03265327
$converged
[1] 0
$nllh.final
[1] 82.07033
attr(,"class")
[1] "gev"表示するにはplotで表示します。
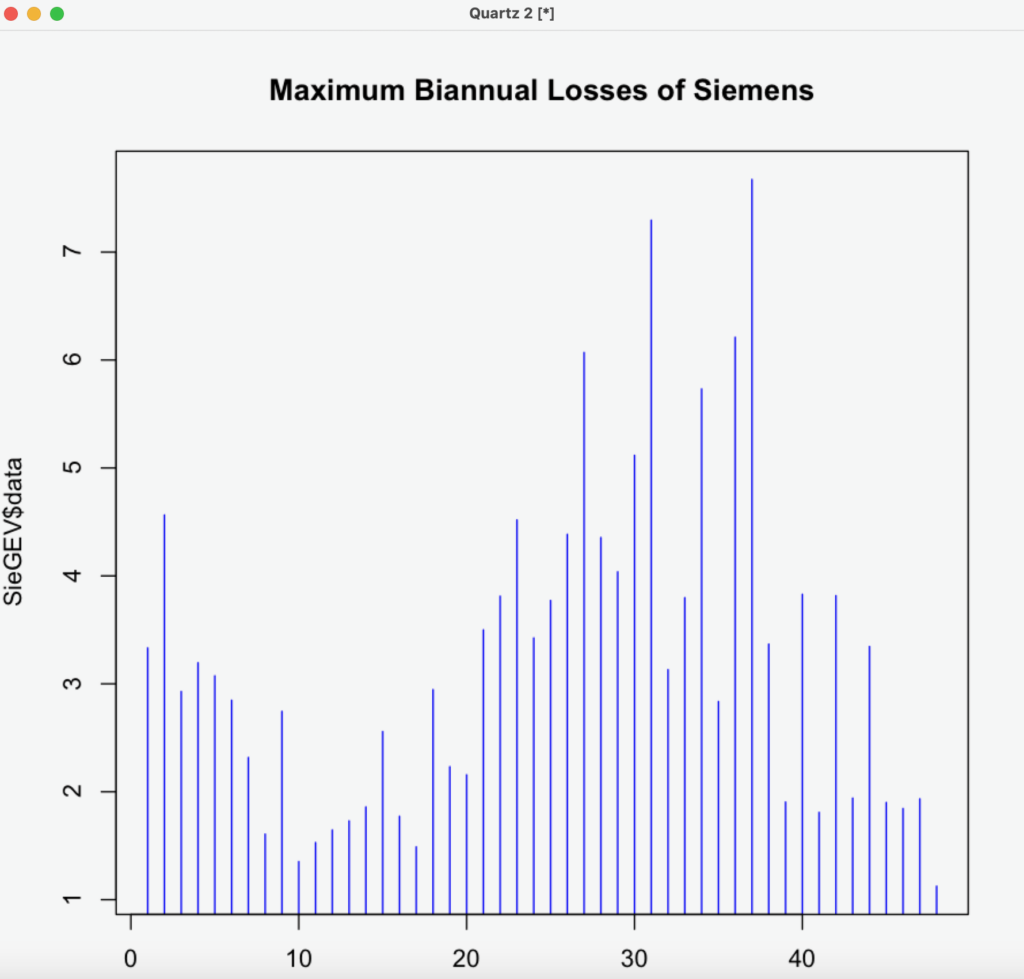
> plot(SieGEV$data,type="h",col="blue", xlab="", main="Maximum Biannual Losses of Siemens")
ismev
ismevを使って gev.fit() gev()が返すパラメータを推定します。
上の図で縦軸にプロットされたevirで得た結果をismevの入力に渡します。
library('ismev')
SieGEV2 <-gev.fit(SieGEV$data)
SieGEV2
> library('ismev')
要求されたパッケージ mgcv をロード中です
要求されたパッケージ nlme をロード中です
次のパッケージを付け加えます: ‘nlme’
以下のオブジェクトは ‘package:dplyr’ からマスクされています:
collapse
This is mgcv 1.8-42. For overview type 'help("mgcv-package")'.
> SieGEV2 <- gev.fit(SieGEV$data)
$conv
[1] 0
$nllh
[1] 82.07033
$mle
[1] 2.443496 1.041265 0.155542
$se
[1] 0.1807022 0.1439107 0.1564440
> SieGEV2
$trans
[1] FALSE
$model
$model[[1]]
NULL
$model[[2]]
NULL
$model[[3]]
NULL
$link
[1] "c(identity, identity, identity)"
$conv
[1] 0
$nllh
[1] 82.07033
$data
[1] 3.332837 4.564551 2.929195 3.195160 3.074342 2.847947 2.317558 1.607382
[9] 2.744829 1.353201 1.529342 1.645970 1.730462 1.859042 2.557895 1.772810
[17] 1.489706 2.946031 2.232120 2.157249 3.500081 3.812336 4.518762 3.425502
[25] 3.772542 4.385188 6.070131 4.355276 4.037816 5.117573 7.295798 3.131371
[33] 3.797925 5.732228 2.836112 6.211146 7.672870 3.368053 1.904819 3.829483
[41] 1.809127 3.817076 1.941525 3.345885 1.900642 1.844945 1.934538 1.125012
$mle
[1] 2.443496 1.041265 0.155542
$cov
[,1] [,2] [,3]
[1,] 0.03265327 0.015389708 -0.012602670
[2,] 0.01538971 0.020710290 -0.007558325
[3,] -0.01260267 -0.007558325 0.024474739
$se
[1] 0.1807022 0.1439107 0.1564440
$vals
[,1] [,2] [,3]
[1,] 2.443496 1.041265 0.155542
[2,] 2.443496 1.041265 0.155542
[3,] 2.443496 1.041265 0.155542
[4,] 2.443496 1.041265 0.155542
[5,] 2.443496 1.041265 0.155542
[6,] 2.443496 1.041265 0.155542
[7,] 2.443496 1.041265 0.155542
[8,] 2.443496 1.041265 0.155542
[9,] 2.443496 1.041265 0.155542
[10,] 2.443496 1.041265 0.155542
[11,] 2.443496 1.041265 0.155542
[12,] 2.443496 1.041265 0.155542
[13,] 2.443496 1.041265 0.155542
[14,] 2.443496 1.041265 0.155542
[15,] 2.443496 1.041265 0.155542
[16,] 2.443496 1.041265 0.155542
[17,] 2.443496 1.041265 0.155542
[18,] 2.443496 1.041265 0.155542
[19,] 2.443496 1.041265 0.155542
[20,] 2.443496 1.041265 0.155542
[21,] 2.443496 1.041265 0.155542
[22,] 2.443496 1.041265 0.155542
[23,] 2.443496 1.041265 0.155542
[24,] 2.443496 1.041265 0.155542
[25,] 2.443496 1.041265 0.155542
[26,] 2.443496 1.041265 0.155542
[27,] 2.443496 1.041265 0.155542
[28,] 2.443496 1.041265 0.155542
[29,] 2.443496 1.041265 0.155542
[30,] 2.443496 1.041265 0.155542
[31,] 2.443496 1.041265 0.155542
[32,] 2.443496 1.041265 0.155542
[33,] 2.443496 1.041265 0.155542
[34,] 2.443496 1.041265 0.155542
[35,] 2.443496 1.041265 0.155542
[36,] 2.443496 1.041265 0.155542
[37,] 2.443496 1.041265 0.155542
[38,] 2.443496 1.041265 0.155542
[39,] 2.443496 1.041265 0.155542
[40,] 2.443496 1.041265 0.155542
[41,] 2.443496 1.041265 0.155542
[42,] 2.443496 1.041265 0.155542
[43,] 2.443496 1.041265 0.155542
[44,] 2.443496 1.041265 0.155542
[45,] 2.443496 1.041265 0.155542
[46,] 2.443496 1.041265 0.155542
[47,] 2.443496 1.041265 0.155542
[48,] 2.443496 1.041265 0.155542
attr(,"class")
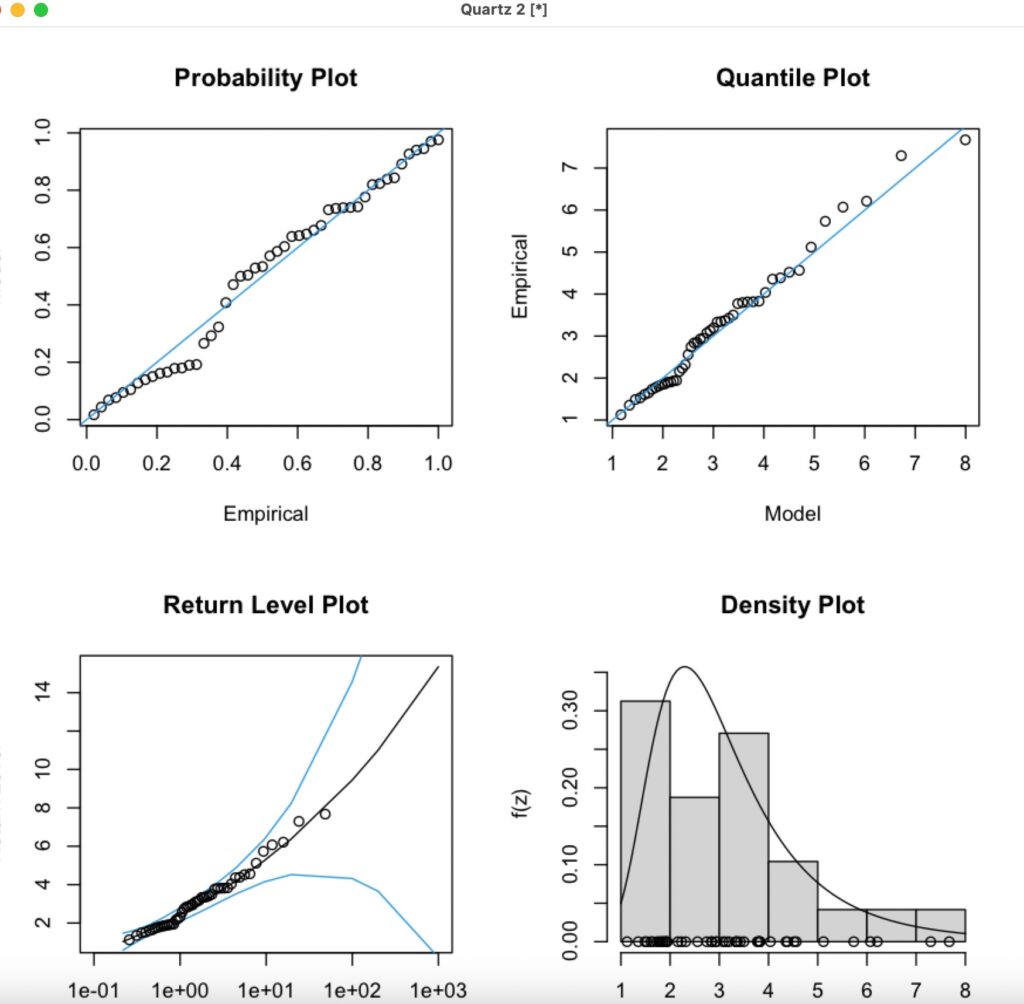
[1] "gev.fit"gev.diag()で表示させます。
> gev.diag(SieGEV2)