2025年2月に合衆国の新政権の政策として、鉄鋼とアルミニウムに25%の関税が課されることが決定されました。一方で、ウクライナへのこれまでの支援の対価として、ウクライナの鉱物資源などの天然資源の権益取得が交渉されています。
この関税政策が、原料である鉄鉱石やボーキサイトなどの鉱物資源の採掘を行なっている企業に与える影響について分析します。
分析手段として機械学習を使った推論手法、DoubleML(Double Machine Learning)を用います。このDoubleMLという推論手法と同じ名称のPythonとRに対応したパッケージ”DoubleML"を使った推論の事例として、マイニング・セクターの代表的な企業の株式のリターンに対するCVaRへの関税の影響を調べます。
自由貿易からの転換
合衆国の新政権による自由貿易主義から保護主義的な政策への転換は、対米貿易に関わる企業が影響を受けます。鉄鋼とアルミニウムに関しては、素材としての鉄鋼、アルミニウムだけでなく、その鉱物資源を扱う企業のビジネスにも影響します。
本稿では鉱物資源の採掘ビジネスを実施している、代表的ないくつかの企業の株式の期待リターンへの国際貿易の環境変化の影響について調べます。
2025年の新関税は実施されたばかりで、評価に用いるサンプルとして利用できるデータがありません。ここで分析の対象にする企業は中国向けの貿易も含めて、世界中で広く採掘と鉱物資源の取引を展開しています。合衆国の現政権の一期目(2018年)の米中の関税の応酬が実施されたときのデータを用いて、事業における関税の影響を調べます。
資産管理では、資産価格の変動に関するリスク指標として、VaR,CVaR(期待ショートフォール)という指標が用いられます。
ある関数のパラメータを推定するのに、一次の線形関数では、スロープをパラメータとして前提しますが、d次元の推定関数のパラメータを推定するのに、LDML(Local Debiased Machine Learning:局所バイアス除去機械学習)というアルゴリズムが提案されています。パラメトリックな関数でモデル化することができない場合に有効に使うことができます。
このLDMアルゴリズムを期待ショートフォール(CVaR)の推定に用いる方法があります。LDMは、DoubleMLという【ylearnによる因果推論】でも取り上げている機械学習を用いた推論の中の一つの方法です。
因果推論と機械学習
因果推論と機械学習の結びつきで応用分野が広がっています。Judea Pearlの推論の梯子のcounterfactualのステージで強化学習(Reinforcement Learning)を使う方法などもいくつか提案されています。
因果推論と機械学習を結びつけたパッケージで、RとPythonで利用できるDoubleMLというパッケージがあります。このライブラリを使って、DMLの事例を見ていきます。
Double/Debiased Machine Learningについて
Double Machine Learningというのは、すべての潜在的な交絡因子と照合基準(収集したデータと観察結果の中で、処置の決定上で同時に直接の効果を持つ因子)が観察されるときに、処置の効果を推定する方法です。しかし、それは従来の統計的なアプローチで適用するのに因子が多すぎるか、または、その処置の効果と結果がパラメトリックな関数でモデル化することができない場合に、それらの問題の両方を機械学習の技術を経由することで記述、説明することができます。
この方法は、最初に二つの予測タスクを推定することで問題の困難さを簡素化します。
- 照合基準(controls)からの結果(outcome)の予測
- 照合基準(controls)から処置(treatment)の予測
最後の推定の段階で、不均一な処置の効果をモデルを作るために、これら二つの予測を組み合わせます。
推定の一般的な手続きは、以下の式で示すとθの推定を実行することです。上の二つの予測タスクは、以下の部分的な線形回帰(partially Linear regression:PLR)モデルを例にとると、
1. Y = D θ0 + g0(X) + U, E[U | X, D] = 0,
2. D = m0(X) + V, E[V | X] = 0, この例で示したPLRモデルの詳細は、以下の論文(1)で紹介されています。
Yは、結果(outcome)変数で、Dが処置(policy/treatment)変数です。ベクターのX=(x1,x2…,xp)が、そのほかの照合(controls)変数から構成されます。U、Vは撹乱因子です。
ビジネスへの応用では、θ0は処置の効果パラメータ、またはリフトパラメータとみなされます。
2番目の式 D =…は、交絡関係を意味します。処置変数は観測基準(control)に依存しています。交絡因子Xは処置(ポリシー)変数Dに関数m0を通じて影響し、関数g0(X)を通して結果変数Yに影響します。
この推論手法と同じ名称を持つDoubleMLというパッケージは、この機械学習の方法を実行するためのライブラリです。Python とRのバージョンがあり、それぞれの機械学習ライブラリ、scikit-learn(Python)とmlr3(R)の上でメタパッケージとしてAPIが実装されています。Conditional ATEを計算するのに、複数のアルゴリズムを利用することができます。
- (1) Robinson, P. M. Root-N-consistent semiparametric regression.
- (2) Victor Chernozhukov, et al. Double/debiased machine learning for treatment and structural parameters.
APT とファクター・モデル
APT(Arbitrage Pricing Theory)では、株式を含む資産のリターンは以下の線形のファクター・モデルで生成されます。
ri = E(ri) + Σ j=1n βijFj + eiE(ri) は、資産iの期待リターン、Fjはj番目のファクター、βijはi番目の資産のそのファクターの感応度、eiは予期されない出来事によりリターンを意味します。
Eugen F. Fama氏とKenneth R. French氏は、マルチファクター・モデルを提案しています。彼らはマクロ経済の指標の代わりに、企業の指標を因子として採用しました。これらの因子がシステミック・リスクをよりよく説明できることを発見したためです。インデックス・モデルを拡張し、企業の規模(SMB)とリターンの生成する因子としてbook-to-market レシオ(HML)を追加しました。
APTモデルを基に3ファクターモデル、と5ファクターモデルを提案しています。
彼らの提案している3ファクターモデルは、以下の式で表せます。
ri - rf = αi + βiM(rM - rf) + βiHML rHML + βiSMB rSMB + eiβiHMLは:i番目の資産の感応度 book-to-market因子、βiSMBは:サイズの因子に対する i番目の資産の感応度、β iM : i番目の株式の 市場インデックス因子へのリスクプレミアム、(rM-rf)はこの因子のリスクプレミアム((インデックス・リターン)- (1ヶ月TBill レイト))、eiは、資産のシステミックではない平均値が0のリスクです。
彼らの3ファクター・モデルのパラメータを、Double MLアルゴリズムの交絡因子として使います。結果(outcome)としての株式のリターンとともに、アルゴリズムへの入力変数になります。
この変数のデータセットは、ダートマス大学のFrench氏のサイトのデータライブラリから、3ファクター・モデルの因子データとしてcsv形式で取得することができます。
ファクター・モデルの因子データの取得
以下のサイトにアクセスし、ファクターモデルの因子データをローカルフォルダにダウンロードしておきます。
https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html
図1 ダートマス大学 French氏のデータライブラリ
大項目 U.S. Research Returns Data ( Downloadable Files)、中項目 Changes in CRSP Dataの項目まで下部にスクロールしてください。
次の図2の画面が表示されます。
図2 Fama/French 3 Factors[Daily]

Changes in CRSP Dataの項目内にある、Fama/French 3 Factors[Daily] csv と表示されている部分をマウスでクリックすると、3ファクターの日次データがダウンロードされます。
ダウンロードしたファイルは、F-F_Research_Data_Factors_daily.csv という名称で保存されます。
データセットの各因子は、X = (X1,...Xp) としてDMLへの制御(controls)変数として使います。
LDML(Local Debiased Machine Learning)アプローチ
QTE(Quantile Treatment Effect)を推定するのは、すべての条件付き累積分布関数、確率的な回帰を推定することを含みます。これは特に、交絡を削除するために条件にする必要のある典型的に膨大な数の共変量のある観測データからなる因果推論に対して、非常に不安定になります。
ここで提案しているLDMLアプローチは、すべての可能な値を推定せずに、単一のθ1の値と、η1(Z,θ1)nuisance関数を推定します。
この方法は、単一のθ1mの値のnuisance関数を推定するだけですが、どのような損失を負うこともありません。さらには、この非常に簡単なnuisanceの推定は、標準的な分類や回帰のタスク処理を減少させることができます。例えば、多くの機械学習法のように、データを既存の条件推定(回帰)、や条件バイナリ確率(分類)に適合させることです。
このアプローチは、どのようにこれらの条件予測関数が推定するかには依存しないので、私たちは、それらを処置するための推定処理をブラックボックスの回帰と分類のアルゴリズムとして既成の機械学習法を使って実行するこができます。
DoubleML model APIにDoubleMLCVARというモデルクラスが定義されています。これはスコア関数にCVARを指定するようになっています。DoubleMLQTEというモデルクラスでは多数のスコア関数が利用できますが、ここではスコア関数にCVARを指定します。
分析の対象とする株式の価格の ヒストリカル・データで調べて、期待ショートフォール(CVaR)の値の変動で、処置の影響(treatment effect)を推定します。(D:ある処置(treatment/policy)以後の資産のリターンの分布をD=1, それ以前の原資産の分布をD=0とみなしてDoubleMLQTEにかけます。)
LDMLアプローチによる期待ショートフォール(CVaR)を調べる対象として、ASX(オーストラリア証券取引所)、NYSEに上場しているUKとオーストラリアの合弁企業の株価データを用います。
今年度の合衆国の新政権による、処置(treatment)としてのTrumpnomicsの影響、鉄鉱、アルミニウムへの輸入関税を考えます。
2018年の関税の応酬を基準に、それ以前のデータを処置(D=0)、それ以後のデータを処置(D=1)とみなして、対象企業の株式のリターンの分布を調べます。制御(controls)変数にFama/French 3ファクター・モデルの因子を使います。
制御変数Xが与えられた時のリターンの分布から期待ショートホール(CVaR)の値を推定します。
- (3) Nathan Kallus, et al. Localized Debiased Machine Learning: Efficient Inference on Quantile Treatment Effects and Beyond
DoubleMLのインストール
オブジェクト指向のDouble/Debiased 機械学習の実装を提供します。機械学習の方法を用いて、nuisance関数を推定します。このライブラリをインストールするには、Python 版は conda、R版は "install.packages()"関数を使います。
- Python版
conda install -c conda-forge doubleml
conda list DoubleML
python -c "import doubleml as dml; print(dml.__version__)"インストールには、パッケージ管理ツールcondaを使います。
conda install -c conda-forge doubleml(base) xxxxxxx$ conda install -c conda-forge doubleml
Retrieving notices: ...working... done
Collecting package metadata (current_repodata.json): done
Solving environment: done
..........DoubleMLのバージョンを確認します。
conda list DoubleML(base) hostnamexxx$ conda list DoubleML
# packages in environment at /opt/anaconda3:
#
# Name Version Build Channel
doubleml 0.9.3 pyhd8ed1ab_0 conda-forgePythonのコードで確認するには
(base) hostnamexxx$ python -c "import doubleml as dml; print(dml.__version__)"
0.9.3インストールパッケージのリストを確認します。
conda listlightgbmがない場合、これもインストールします。
conda install lightgbm(base) xxxxxxx$ conda install lightgbm
Collecting package metadata (current_repodata.json): done
Solving environment: done
...- R版
Rを起動した状態で、Rのコマンドプロンプトから、以下のinstall.packages()コマンドを使います。
install.packages("DoubleML")
library(DoubleML)データの準備
処置変数として、合衆国政府の関税の実施を変数にとります。関税がある場合をD=1, 関税前の観測値をD=0とみなしてデータを取り扱います。
関税の実施を処置変数Dとして、パラメータ化することが適当か検討の余地がありますが、Fama-Frenchの3ファクターが市場全体の振る舞いを反映しているとみなせば、3ファクターとDの値が連動すると見なせます。
本稿では、DoubleMLを使った推論の事例として、実際の市場経済における関税と上場株式の期待リターンの関係を推論の対象にします。
制御(controls)変数のデータセットとして、Fama/Frenchの3ファクター・モデルのデータセット(Mkt-rf,SMB,HML,rf)を用います。
結果(outcome)としての観測値は、ASX(オーストラリア証券取引所)、LSE(ロンドン証券取引所)、NYSEに上場されている、鉱物資源を扱うUK、オーストラリア合弁企業であるA社とB社の株価データを使います。株式の期待リターンが変数Yに相当します。データセットの期間は、2016年1月〜2019年12月までとします。2020年のCOVID19の影響を排除したいためです。
リソースの異なる二つのデータセットの日付のずれがないように、3ファクター・モデルのデータセットと株価データの日付の並びを対応させておきます。
A社のOHLC形式の株価データを基にnew1.csvという名称のファイル、F-F_Research_Data_Factors_daily.csvを基にnew2.csvという名称のファイルを作りました。二つのファイルのindexと日付は対応し、データセットのサイズも一致させています。このファイルをpandasのデータフレームに読み込みます。
以下の図3は、2016年1月4日から2020年12月31日までのA社の株価のOHLC形式のデータです。Pandasのデータフレームのフォーマットで、最後の列(’ret’)に日次リターンを計算してセットしています。
図3 A社株式データ
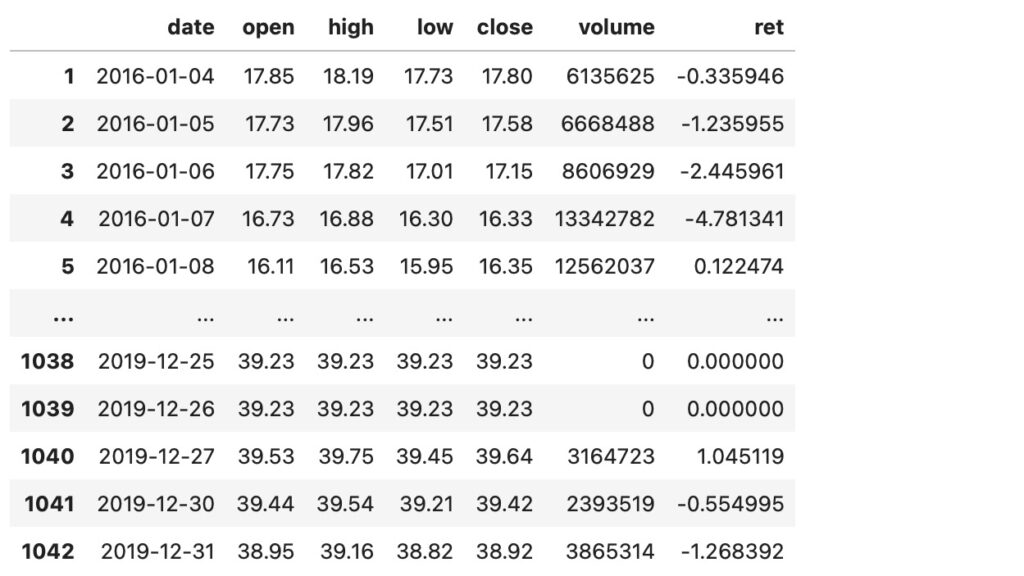
これはpandasのデータフレームですが、DMLのデータオブジェクトの引数として渡す場合は、numpyの配列に変換します。q1をpandasデータフレームとすると、以下のようにyをnumpyの変数に変換し、基準の日付(2018/02/01)からデータセットを二つに分割します。
y = q1['ret'].to_numpy()
#20180201 as tr-date
y0 = y[:543]
y1 = y[544:]y0とy1に対しての分位点での分布の累積リターンを計算しておきます。
tau_vec = np.arange(0.1,0.95,0.05)
Y0_quant = np.quantile(y0, q=tau_vec)
Y0_cvar = [y0[y0 >= quant].mean() for quant in Y0_quant]
print(f'Conditional Value at Risk Y(0): {Y0_cvar}')Conditional Value at Risk Y(0): [0.48617085189704207, 0.6242289535856921, 0.7476691595169653, 0.8685592099641457, 0.9830762392189896, 1.0990422662082289, 1.2146887619723092, 1.332091681374479, 1.4679443193768684, 1.6084619438009926, 1.7585621235263122, 1.9237819469339266, 2.1067436318380577, 2.321429984787155, 2.5710164358198417, 2.8837938282803988, 3.2923441794291395]Y1_quant = np.quantile(y1, q=tau_vec)
Y1_cvar = [y1[y1 >= quant].mean() for quant in Y1_quant]
print(f'Conditional Value at Risk Y(1): {Y1_cvar}')Conditional Value at Risk Y(1): [0.38509992505592555, 0.4967314596139056, 0.5969694475659114, 0.6949554197397257, 0.7921485648678442, 0.8835237819402357, 0.973603998874989, 1.0324631767403818, 1.1696942924680427, 1.277558909840987, 1.3931796579159428, 1.5196101636599062, 1.6539948920531562, 1.8121912063416956, 1.9900127429893493, 2.2013566528399227, 2.4838884943271125]図4は、A社の株価データと同期間のFama/French 3ファクターのデータセットです。
図4 Fama/French 3ファクター
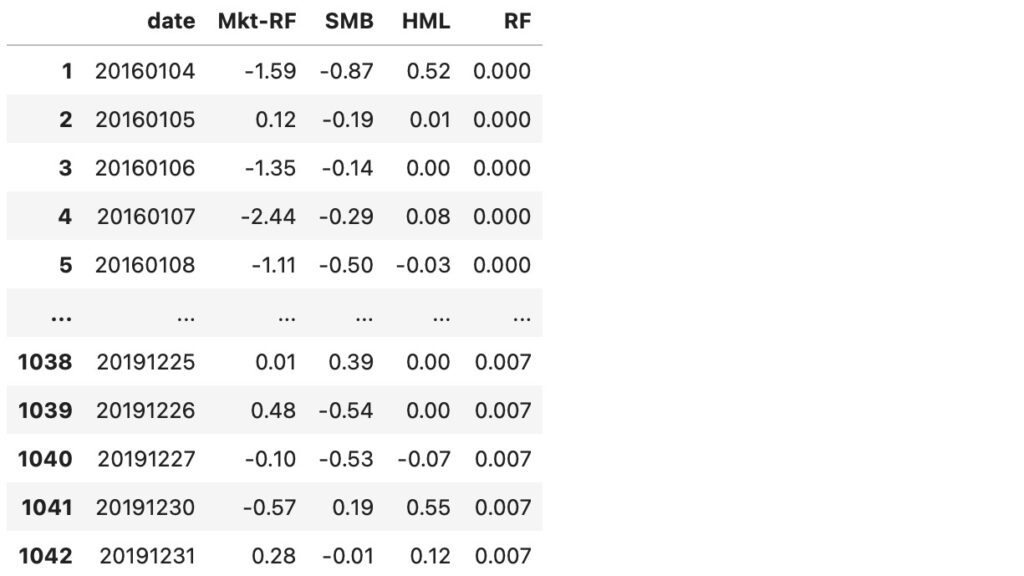
図5は、図4のデータから日付の列を削除したデータです。
dx = d2.drop(columns='date')
dx図5 Fama/French 3ファクター 日付削除
このPandasのデータフレームをnumpyの配列に変換し、DMLに渡します。
xdata = dx.to_numpy()
xdataarray([[-1.59 , -0.87 , 0.52 , 0. ],
[ 0.12 , -0.19 , 0.01 , 0. ],
[-1.35 , -0.14 , 0. , 0. ],
...,
[-0.1 , -0.53 , -0.07 , 0.007],
[-0.57 , 0.19 , 0.55 , 0.007],
[ 0.28 , -0.01 , 0.12 , 0.007]])Treatment Dを設定します。配列の0..544までが期間2016/01/04〜2018/02/28に対応しています。
d1= np.zeros((544), dtype='i', order='C')
d2= np.ones((498), dtype='i', order='C')
d = np.append(d1,d2)
darray([0, 0, 0, ..., 1, 1, 1], dtype=int32)DMLのデータオブジェクトを生成し、データをセットします。yは図3の株価データの’ret’列、日次のリターンです。
obj_dml_data = dml.DoubleMLData.from_arrays(xdata, y, d)これで、DMLで取り扱うオブジェクトの形式に各データが変換されました。このオブジェクトに対して、DoubleMLのAPIを適用していきます。
DML CVaRの推定
CVaRクラスに定義されているAPIを使います。
データセットを分位点で分割し、処置0、1に対して評価関数としてCVaRを適用して学習させます。
回帰と分類のアルゴリズムには、それぞれ、RandomForestRegressorとRandomForestClassifierを用いています。
LDMLは、直接、既存の機械学習のメソッドを使って、ブラックボックスの回帰と分類アルゴリズム(ランダム・フォレスト、グラジェント・ブースティング、ニューラルネットワーク)としてそれらを処置します。アルゴリズムは内部処理をブラックボックスとして扱えるため、既存の機械学習メソッドが選択できます。
結果がCVAR_0, CVAR_1に格納されます。分位点毎にCVaRを計算します。
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
np.random.seed(3141)
ml_g = RandomForestRegressor(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
ml_m = RandomForestClassifier(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
CVAR_0 = np.full((len(tau_vec)), np.nan)
CVAR_1 = np.full((len(tau_vec)), np.nan)
ci_CVAR_0 = np.full((len(tau_vec),2), np.nan)
ci_CVAR_1 = np.full((len(tau_vec),2), np.nan)
for idx_tau, tau in enumerate(tau_vec):
print(f'Quantile: {tau}')
dml_CVAR_0 = dml.DoubleMLCVAR(obj_dml_data,
ml_g, ml_m,
quantile=tau,
treatment=0,
n_folds=5)
dml_CVAR_1 = dml.DoubleMLCVAR(obj_dml_data,
ml_g, ml_m,
quantile=tau,
treatment=1,
n_folds=5)
dml_CVAR_0.fit()
dml_CVAR_1.fit()
ci_CVAR_0[idx_tau, :] = dml_CVAR_0.confint(level=0.95).to_numpy()
ci_CVAR_1[idx_tau, :] = dml_CVAR_1.confint(level=0.95).to_numpy()
CVAR_0[idx_tau] = dml_CVAR_0.coef.squeeze()
CVAR_1[idx_tau] = dml_CVAR_1.coef.squeeze()Quantile: 0.1
Quantile: 0.15000000000000002
Quantile: 0.20000000000000004
Quantile: 0.25000000000000006
Quantile: 0.30000000000000004
Quantile: 0.3500000000000001
Quantile: 0.40000000000000013
Quantile: 0.4500000000000001
Quantile: 0.5000000000000001
Quantile: 0.5500000000000002
Quantile: 0.6000000000000002
Quantile: 0.6500000000000001
Quantile: 0.7000000000000002
Quantile: 0.7500000000000002
Quantile: 0.8000000000000003
Quantile: 0.8500000000000003
Quantile: 0.9000000000000002【1.】A社のCVaR 推定
結果を表示してみます。
data = {"Quantile": tau_vec, "CVaR Y(0)": Y0_cvar, "CVaR Y(1)": Y1_cvar,
"DML CVaR Y(0)": CVAR_0, "DML CVaR Y(1)": CVAR_1,
"DML CVaR Y(0) lower": ci_CVAR_0[:, 0], "DML CVaR Y(0) upper": ci_CVAR_0[:, 1],
"DML CVaR Y(1) lower": ci_CVAR_1[:, 0], "DML CVaR Y(1) upper": ci_CVAR_1[:, 1]}
df = pd.DataFrame(data)
print(df) Quantile CVaR Y(0) CVaR Y(1) DML CVaR Y(0) DML CVaR Y(1) \
0 0.10 0.486171 0.385100 0.505234 0.388853
1 0.15 0.624229 0.496731 0.615008 0.498950
2 0.20 0.747669 0.596969 0.758611 0.708970
3 0.25 0.868559 0.694955 0.967893 0.731765
4 0.30 0.983076 0.792149 1.009982 0.831497
5 0.35 1.099042 0.883524 1.008584 0.972638
6 0.40 1.214689 0.973604 1.182320 1.045817
7 0.45 1.332092 1.032463 1.254614 1.135964
8 0.50 1.467944 1.169694 1.418600 1.244710
9 0.55 1.608462 1.277559 1.546307 1.385771
10 0.60 1.758562 1.393180 1.646027 1.412054
11 0.65 1.923782 1.519610 1.855480 1.639435
12 0.70 2.106744 1.653995 3.836887 1.730321
13 0.75 2.321430 1.812191 2.171069 1.862014
14 0.80 2.571016 1.990013 3.420814 2.154158
15 0.85 2.883794 2.201357 2.915141 2.317265
16 0.90 3.292344 2.483888 3.418578 2.675943
DML CVaR Y(0) lower DML CVaR Y(0) upper DML CVaR Y(1) lower \
0 0.345436 0.665032 0.261335
1 0.431893 0.798124 0.366383
2 0.594062 0.923160 0.578470
3 0.756112 1.179673 0.586415
4 0.674636 1.345327 0.694416
5 0.774920 1.242248 0.824867
6 0.999428 1.365212 0.910170
7 0.990878 1.518350 0.991545
8 1.226389 1.610812 1.094883
9 1.335661 1.756953 1.172925
10 1.416263 1.875792 1.254660
11 1.626221 2.084740 1.458147
12 3.546504 4.127271 1.558670
13 1.699061 2.643076 1.658728
14 2.084152 4.757476 1.942581
15 2.549697 3.280585 2.101239
16 3.082861 3.754295 2.389533
DML CVaR Y(1) upper
0 0.516371
1 0.631518
2 0.839470
3 0.877115
4 0.968578
5 1.120408
6 1.181464
7 1.280382
8 1.394537
9 1.598617
10 1.569449
11 1.820723
12 1.901972
13 2.065301
14 2.365735
15 2.533292
16 2.962354 matplotlibで視覚化します。
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = 10., 7.5
fig, (ax1, ax2) = plt.subplots(1 ,2)
ax1.grid(); ax2.grid()
ax1.plot(df['Quantile'],df['DML CVaR Y(0)'], color='violet', label='Estimated CVaR Y(0)')
ax1.plot(df['Quantile'],df['CVaR Y(0)'], color='green', label='True CVaR Y(0)')
ax1.fill_between(df['Quantile'], df['DML CVaR Y(0) lower'], df['DML CVaR Y(0) upper'], color='violet', alpha=.3, label='Confidence Interval')
ax1.legend()
ax1.set_ylim(0, 5)
ax2.plot(df['Quantile'],df['DML CVaR Y(1)'], color='violet', label='Estimated CVaR Y(1)')
ax2.plot(df['Quantile'],df['CVaR Y(1)'], color='green', label='True CVaR Y(1)')
ax2.fill_between(df['Quantile'], df['DML CVaR Y(1) lower'], df['DML CVaR Y(1) upper'], color='violet', alpha=.3, label='Confidence Interval')
ax2.legend()
ax2.set_ylim(0, 5)
fig.suptitle('Conditional Value at Risk', fontsize=16)
fig.supxlabel('Quantile')
_ = fig.supylabel('CVaR and 95%-CI')図6 期待ショートフォール(CVaR) A社
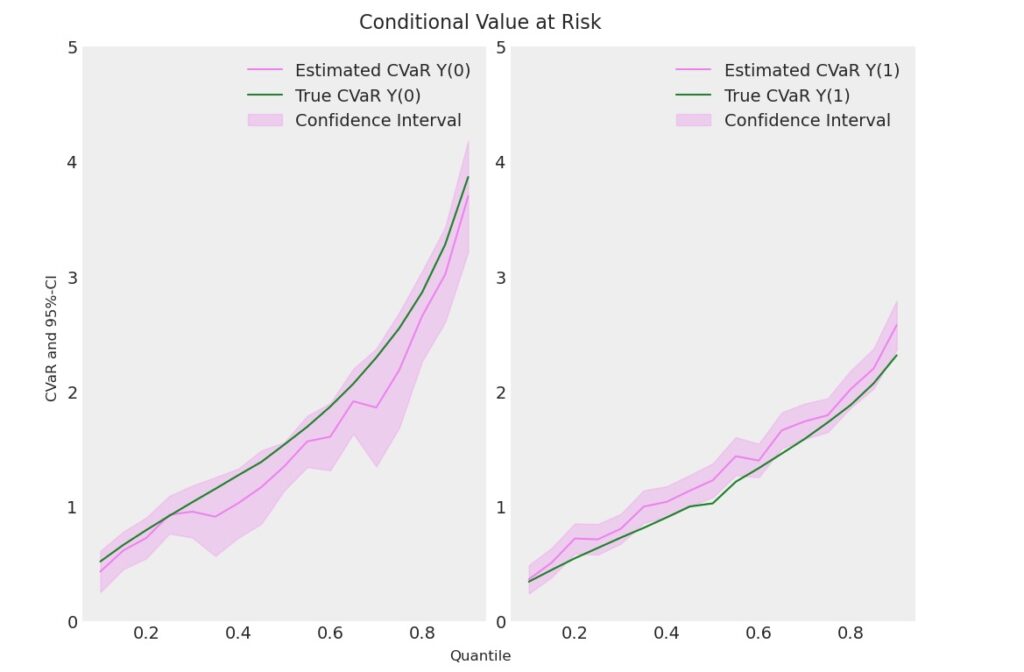
CVaRの機械学習による推定値は実測値に近い値を出力しています。
DML QTEによる推定 CVaR
次にQTEによる推定を計算します。機械学習メソッドは、ランダム・フォレスト、Neyman スコア関数には'CVaR'を指定します。
ml_g = RandomForestRegressor(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
ml_m = RandomForestClassifier(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
n_cores = multiprocessing.cpu_count()
cores_used = np.min([5, n_cores - 1])
print(f"Number of Cores used: {cores_used}")
dml_CVAR = dml.DoubleMLQTE(obj_dml_data,
ml_g,
ml_m,
score='CVaR',
quantiles=tau_vec,
n_folds=5)
dml_CVAR.fit(n_jobs_models=cores_used)
print(dml_CVAR)Number of Cores used: 5
================== DoubleMLQTE Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % 97.5 %
0.10 -0.046660 0.111800 -0.417355 6.764188e-01 -0.265784 0.172463
0.15 -0.114901 0.121308 -0.947186 3.435439e-01 -0.352659 0.122858
0.20 -0.064197 0.110296 -0.582043 5.605375e-01 -0.280373 0.151979
0.25 -0.105695 0.112258 -0.941535 3.464307e-01 -0.325717 0.114327
0.30 -0.085658 0.118168 -0.724885 4.685227e-01 -0.317262 0.145946
0.35 -0.011427 0.158849 -0.071936 9.426525e-01 -0.322766 0.299912
0.40 -0.118421 0.123809 -0.956479 3.388302e-01 -0.361082 0.124241
0.45 -0.132255 0.126053 -1.049205 2.940837e-01 -0.379314 0.114804
0.50 -0.142488 0.133207 -1.069675 2.847657e-01 -0.403568 0.118592
0.55 -0.120862 0.142999 -0.845194 3.980027e-01 -0.401134 0.159411
0.60 -0.146108 0.146598 -0.996661 3.189291e-01 -0.433434 0.141218
0.65 -0.167924 0.160391 -1.046965 2.951158e-01 -0.482284 0.146437
0.70 -0.339107 0.149911 -2.262056 2.369392e-02 -0.632927 -0.045287
0.75 -0.827495 0.157326 -5.259739 1.442600e-07 -1.135849 -0.519141
0.80 -2.582946 0.459392 -5.622534 1.881770e-08 -3.483337 -1.682554
0.85 -0.392458 1.030514 -0.380837 7.033244e-01 -2.412227 1.627312
0.90 -0.411093 0.454540 -0.904415 3.657755e-01 -1.301975 0.479790 QTEクラスのAPIのブートストラップ・メソッドを使って、2000サンプル生成し、信頼区間の計算に使います。ブートストラップ法は、サンプル数が少ない時に、元データからサンプルを生成する場合に利用できます(注1)。QTEクラスのconfint()メソッドを使って正しい信頼区間が設定できます。
(注1:QTEとは別な統計処理で、株価のリターンをブートストラップ法で5000サンプリングした例を図8、図9に示します。)
ci_CVAR = dml_CVAR.confint(level=0.95, joint=False)
dml_CVAR.bootstrap(n_rep_boot=2000)
ci_joint_CVAR = dml_CVAR.confint(level=0.95, joint=True)
print(ci_joint_CVAR) 2.5 % 97.5 %
0.10 -0.330517 0.237196
0.15 -0.422897 0.193096
0.20 -0.344235 0.215841
0.25 -0.390715 0.179325
0.30 -0.385682 0.214366
0.35 -0.414741 0.391887
0.40 -0.432769 0.195927
0.45 -0.452300 0.187789
0.50 -0.480695 0.195720
0.55 -0.483932 0.242209
0.60 -0.518315 0.226099
0.65 -0.575151 0.239304
0.70 -0.719726 0.041513
0.75 -1.226942 -0.428048
0.80 -3.749329 -1.416563
0.85 -3.008904 2.223989
0.90 -1.565158 0.742972結果を表示します。
結果の平均と処置の結果の平均(ATE)を比較します。QTEはより堅牢な処置の影響を提供します。予測した処置の影響と実際の処置の結果を比較します。
潜在的な結果は観測せず、Y=Y(T)の実測値だけの結果が現れます。 Z=(X ,T,Y)
CVAR = np.array(Y1_cvar) - np.array(Y0_cvar)
data = {"Quantile": tau_vec, "CVaR": CVAR, "DML CVaR": dml_CVAR.coef,
"DML CVaR pointwise lower": ci_CVAR['2.5 %'], "DML CVaR pointwise upper": ci_CVAR['97.5 %'],
"DML CVaR joint lower": ci_joint_CVAR['2.5 %'], "DML CVaR joint upper": ci_joint_CVAR['97.5 %']}
df = pd.DataFrame(data)
print(df) Quantile CVaR DML CVaR DML CVaR pointwise lower \
0.10 0.10 -0.101071 -0.046660 -0.265784
0.15 0.15 -0.127497 -0.114901 -0.352659
0.20 0.20 -0.150700 -0.064197 -0.280373
0.25 0.25 -0.173604 -0.105695 -0.325717
0.30 0.30 -0.190928 -0.085658 -0.317262
0.35 0.35 -0.215518 -0.011427 -0.322766
0.40 0.40 -0.241085 -0.118421 -0.361082
0.45 0.45 -0.299629 -0.132255 -0.379314
0.50 0.50 -0.298250 -0.142488 -0.403568
0.55 0.55 -0.330903 -0.120862 -0.401134
0.60 0.60 -0.365382 -0.146108 -0.433434
0.65 0.65 -0.404172 -0.167924 -0.482284
0.70 0.70 -0.452749 -0.339107 -0.632927
0.75 0.75 -0.509239 -0.827495 -1.135849
0.80 0.80 -0.581004 -2.582946 -3.483337
0.85 0.85 -0.682437 -0.392458 -2.412227
0.90 0.90 -0.808456 -0.411093 -1.301975
DML CVaR pointwise upper DML CVaR joint lower DML CVaR joint upper
0.10 0.172463 -0.330517 0.237196
0.15 0.122858 -0.422897 0.193096
0.20 0.151979 -0.344235 0.215841
0.25 0.114327 -0.390715 0.179325
0.30 0.145946 -0.385682 0.214366
0.35 0.299912 -0.414741 0.391887
0.40 0.124241 -0.432769 0.195927
0.45 0.114804 -0.452300 0.187789
0.50 0.118592 -0.480695 0.195720
0.55 0.159411 -0.483932 0.242209
0.60 0.141218 -0.518315 0.226099
0.65 0.146437 -0.575151 0.239304
0.70 -0.045287 -0.719726 0.041513
0.75 -0.519141 -1.226942 -0.428048
0.80 -1.682554 -3.749329 -1.416563
0.85 1.627312 -3.008904 2.223989
0.90 0.479790 -1.565158 0.742972 matplotlibで視覚化します。
plt.rcParams['figure.figsize'] = 10., 7.5
fig, ax = plt.subplots()
ax.grid()
ax.plot(df['Quantile'],df['DML CVaR'], color='violet', label='Estimated CVaR')
ax.plot(df['Quantile'],df['CVaR'], color='green', label='True CVaR')
ax.fill_between(df['Quantile'], df['DML CVaR pointwise lower'], df['DML CVaR pointwise upper'], color='violet', alpha=.3, label='Pointwise Confidence Interval')
ax.fill_between(df['Quantile'], df['DML CVaR joint lower'], df['DML CVaR joint upper'], color='violet', alpha=.2, label='Joint Confidence Interval')
plt.legend()
plt.title('Conditional Value at Risk', fontsize=16)
plt.xlabel('Quantile')
_ = plt.ylabel('QTE and 95%-CI')図7 QTEによるCVaRの推定 A社
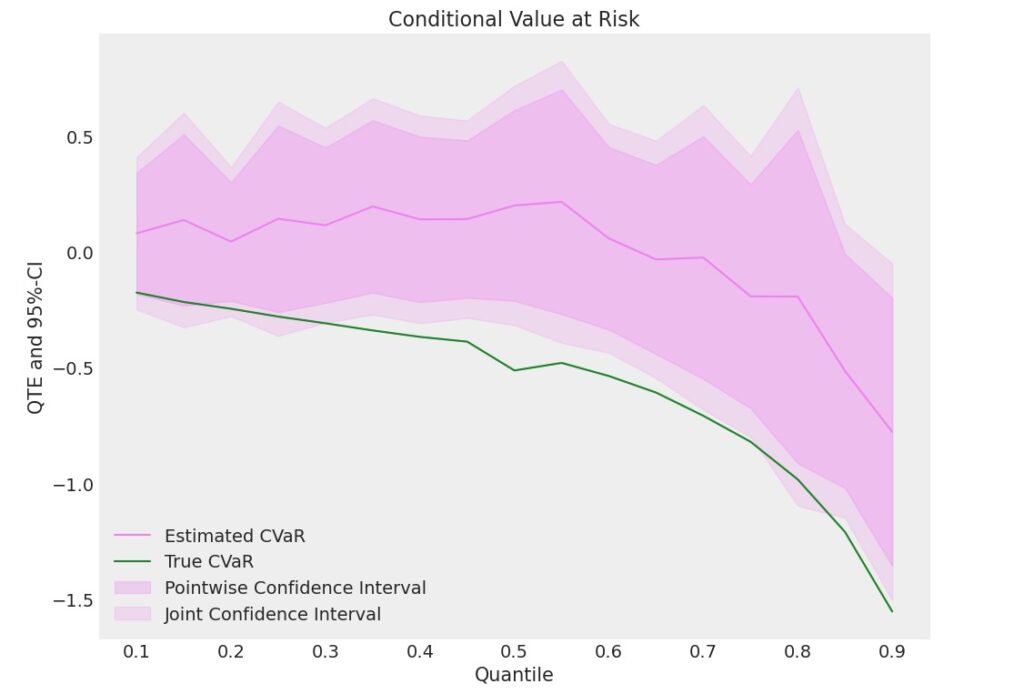
D=1、関税実施後の方がリターンの平均が小さいため、分布の累積のCVaRの値が小さくなります。信頼区間95%の頻度で、大きく損失が発生するリスクは小さくなりますが、期待リターンも小さくなっています。そのため、分布の累積、CVaRは区間の上位に向かうほど小さくなっています。
以下は、ブートストラップ法を使って、5000サンプリングしたD=0(2016/1~2018/1)とD=1(2018/2~2019/12)の期間のリターンの分布です。
以下の図8の期待リターンの平均が、図9ではマイナス方向にシフトしているのと、分散が小さくなっていることがわかります。
図8 ブートストラップ法によるリターンの分布 A社(2016/01/04~2018/01/31)
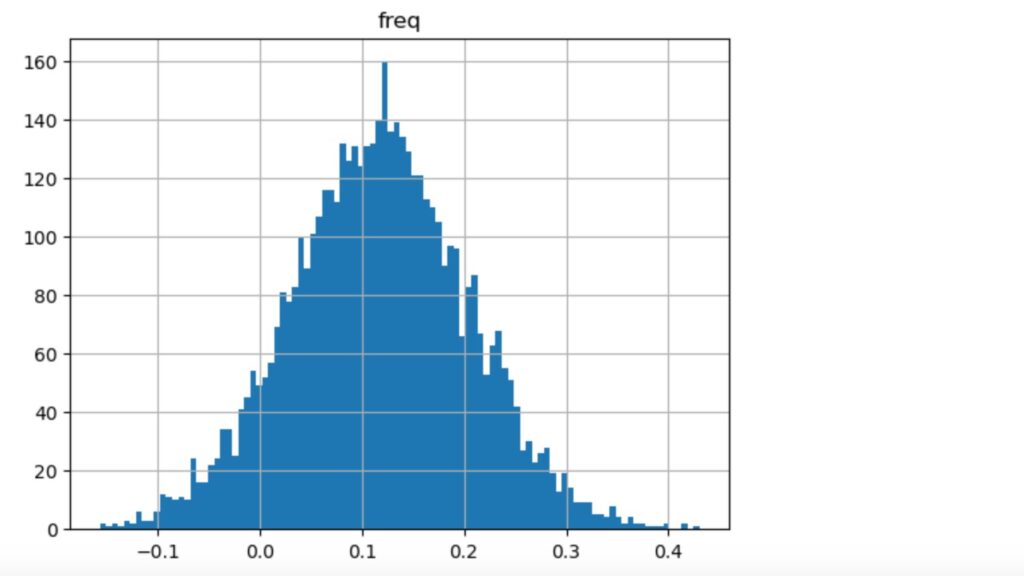
図9 ブートストラップによるリターンの分布 A社(2018/02/01~2019/12/31)
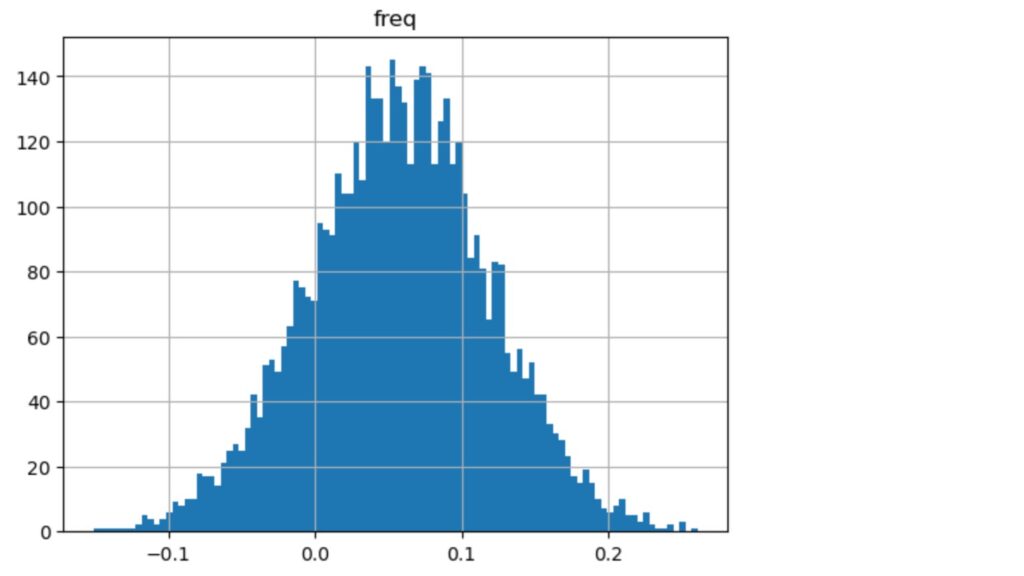
95%の信頼区間でのダウンサイド・リスクは変わりませんが、処置後の期待リターンの分布の平均値が左にシフトし、期待リターンは減少しています。
A社のCVaRの推定と同様の推定を、B社対して実施します。
【2】B社のCVaR推定
B社の株価データを使って推定します。
図10 B社の株価のOHLCデータ、最後の列は日次リターン
B社のデータセットをオブジェクトにセットします。
obj_dml_data = dml.DoubleMLData.from_arrays(xdata, y, d) 回帰関数と分類関数に、それぞれ、RandomForestRegressorとRandomForestClassifierを使います。
分位点毎に学習します。
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
np.random.seed(431)
ml_g = RandomForestRegressor(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
ml_m = RandomForestClassifier(n_estimators=100, max_features=20, max_depth=10, min_samples_leaf=2)
CVAR_0 = np.full((len(tau_vec)), np.nan)
CVAR_1 = np.full((len(tau_vec)), np.nan)
ci_CVAR_0 = np.full((len(tau_vec),2), np.nan)
ci_CVAR_1 = np.full((len(tau_vec),2), np.nan)
for idx_tau, tau in enumerate(tau_vec):
print(f'Quantile: {tau}')
dml_CVAR_0 = dml.DoubleMLCVAR(obj_dml_data,
ml_g, ml_m,
quantile=tau,
treatment=0,
n_folds=5)
dml_CVAR_1 = dml.DoubleMLCVAR(obj_dml_data,
ml_g, ml_m,
quantile=tau,
treatment=1,
n_folds=5)
dml_CVAR_0.fit()
dml_CVAR_1.fit()
ci_CVAR_0[idx_tau, :] = dml_CVAR_0.confint(level=0.95).to_numpy()
ci_CVAR_1[idx_tau, :] = dml_CVAR_1.confint(level=0.95).to_numpy()
CVAR_0[idx_tau] = dml_CVAR_0.coef.squeeze()
CVAR_1[idx_tau] = dml_CVAR_1.coef.squeeze()Quantile: 0.1
Quantile: 0.15000000000000002
Quantile: 0.20000000000000004
Quantile: 0.25000000000000006
Quantile: 0.30000000000000004
Quantile: 0.3500000000000001
Quantile: 0.40000000000000013
Quantile: 0.4500000000000001
Quantile: 0.5000000000000001
Quantile: 0.5500000000000002
Quantile: 0.6000000000000002
Quantile: 0.6500000000000001
Quantile: 0.7000000000000002
Quantile: 0.7500000000000002
Quantile: 0.8000000000000003
Quantile: 0.8500000000000003
Quantile: 0.9000000000000002結果を表示します。
data = {"Quantile": tau_vec, "CVaR Y(0)": Y0_cvar, "CVaR Y(1)": Y1_cvar,
"DML CVaR Y(0)": CVAR_0, "DML CVaR Y(1)": CVAR_1,
"DML CVaR Y(0) lower": ci_CVAR_0[:, 0], "DML CVaR Y(0) upper": ci_CVAR_0[:, 1],
"DML CVaR Y(1) lower": ci_CVAR_1[:, 0], "DML CVaR Y(1) upper": ci_CVAR_1[:, 1]}
df = pd.DataFrame(data)
print(df)
Quantile CVaR Y(0) CVaR Y(1) DML CVaR Y(0) DML CVaR Y(1) \
0 0.10 0.605445 0.378206 0.567861 0.416520
1 0.15 0.763471 0.507202 0.749781 0.520552
2 0.20 0.911639 0.616900 0.988235 0.673720
3 0.25 1.053052 0.714615 1.062879 0.767037
4 0.30 1.189674 0.807920 1.149432 0.868956
5 0.35 1.328312 0.895962 1.255045 0.952732
6 0.40 1.467723 0.989265 1.552000 1.109898
7 0.45 1.575559 1.085836 1.463335 1.123996
8 0.50 1.770319 1.194291 1.749544 1.326600
9 0.55 1.940115 1.315347 1.906569 1.517453
10 0.60 2.124723 1.444757 2.114632 1.554796
11 0.65 2.334260 1.590505 2.080623 1.736980
12 0.70 2.581594 1.738267 2.367640 1.803286
13 0.75 2.873662 1.911839 2.848699 2.153645
14 0.80 3.242005 2.122675 3.140657 2.460762
15 0.85 3.728167 2.389335 3.730591 3.479617
16 0.90 4.423553 2.790636 4.119367 2.945898
DML CVaR Y(0) lower DML CVaR Y(0) upper DML CVaR Y(1) lower \
0 0.371772 0.763950 0.282715
1 0.561021 0.938540 0.394193
2 0.757268 1.219202 0.544626
3 0.836781 1.288976 0.633402
4 0.972489 1.326375 0.734875
5 1.046893 1.463198 0.816271
6 1.354488 1.749511 0.972384
7 1.167015 1.759654 0.977238
8 1.509978 1.989110 1.154694
9 1.665149 2.147989 1.351807
10 1.837490 2.391775 1.375539
11 1.766419 2.394827 1.548404
12 1.951542 2.783737 1.611157
13 2.478563 3.218835 1.928984
14 2.563818 3.717496 2.217331
15 3.263982 4.197201 3.246070
16 3.168129 5.070606 2.611468
DML CVaR Y(1) upper
0 0.550325
1 0.646911
2 0.802814
3 0.900671
4 1.003037
5 1.089193
6 1.247411
7 1.270755
8 1.498505
9 1.683098
10 1.734052
11 1.925556
12 1.995415
13 2.378307
14 2.704193
15 3.713163
16 3.280329 matplotlibで視覚化します。
図11 期待ショートフォール(CVaR) B社
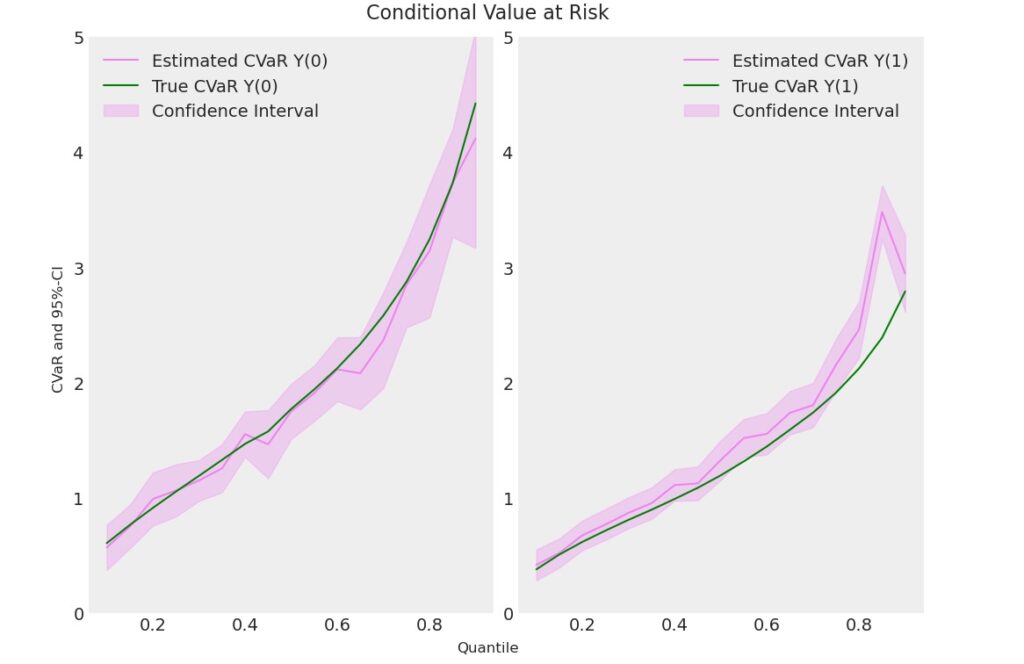
図11の右側の処置後のCVaRに推定値に、分位点が0.8近辺で、推定値がうまく学習されていません。出力結果からは、quantileの15番目でCVaR (Y1)の値が外れています。サンプル数が少ないことが関係しているのか、この推定の外れ値の理由がはっきりしません。(調査中)
次に、DoubleMLQTEクラスのAPIを使います。スコア関数に'CVaR'を指定します。
Number of Cores used: 5
================== DoubleMLQTE Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % 97.5 %
0.10 -0.340022 0.127501 -2.666820 0.007657 -0.589919 -0.090125
0.15 -0.314659 0.115846 -2.716179 0.006604 -0.541714 -0.087605
0.20 -0.277367 0.115073 -2.410352 0.015937 -0.502907 -0.051828
0.25 -0.420466 0.135889 -3.094181 0.001974 -0.686803 -0.154128
0.30 -0.422968 0.122280 -3.458995 0.000542 -0.662633 -0.183302
0.35 -0.424047 0.149086 -2.844312 0.004451 -0.716249 -0.131844
0.40 -0.508902 0.131162 -3.879958 0.000104 -0.765974 -0.251830
0.45 -0.510108 0.124150 -4.108794 0.000040 -0.753438 -0.266778
0.50 -0.474239 0.140018 -3.386996 0.000707 -0.748669 -0.199810
0.55 -0.481834 0.138851 -3.470147 0.000520 -0.753977 -0.209691
0.60 -0.493705 0.157936 -3.125976 0.001772 -0.803254 -0.184156
0.65 -0.465395 0.194050 -2.398327 0.016470 -0.845726 -0.085064
0.70 -0.594140 0.221552 -2.681722 0.007324 -1.028373 -0.159907
0.75 -0.701311 0.258945 -2.708335 0.006762 -1.208835 -0.193787
0.80 -0.951205 0.322979 -2.945103 0.003228 -1.584232 -0.318179
0.85 -1.221626 0.283849 -4.303787 0.000017 -1.777960 -0.665292
0.90 -0.654325 0.316273 -2.068862 0.038559 -1.274208 -0.034441ブートストラップのサンプリング結果です。
2.5 % 97.5 %
0.10 -0.666174 -0.013869
0.15 -0.610999 -0.018319
0.20 -0.571730 0.016995
0.25 -0.768076 -0.072855
0.30 -0.735766 -0.110169
0.35 -0.805415 -0.042679
0.40 -0.844419 -0.173384
0.45 -0.827690 -0.192526
0.50 -0.832411 -0.116068
0.55 -0.837021 -0.126647
0.60 -0.897713 -0.089697
0.65 -0.961784 0.030993
0.70 -1.160878 -0.027401
0.75 -1.363705 -0.038917
0.80 -1.777399 -0.125012
0.85 -1.947724 -0.495528
0.90 -1.463364 0.154715結果を表示します。
Quantile CVaR DML CVaR DML CVaR pointwise lower \
0.10 0.10 -0.227239 -0.340022 -0.589919
0.15 0.15 -0.256268 -0.314659 -0.541714
0.20 0.20 -0.294739 -0.277367 -0.502907
0.25 0.25 -0.338438 -0.420466 -0.686803
0.30 0.30 -0.381754 -0.422968 -0.662633
0.35 0.35 -0.432350 -0.424047 -0.716249
0.40 0.40 -0.478457 -0.508902 -0.765974
0.45 0.45 -0.489724 -0.510108 -0.753438
0.50 0.50 -0.576028 -0.474239 -0.748669
0.55 0.55 -0.624768 -0.481834 -0.753977
0.60 0.60 -0.679966 -0.493705 -0.803254
0.65 0.65 -0.743755 -0.465395 -0.845726
0.70 0.70 -0.843328 -0.594140 -1.028373
0.75 0.75 -0.961823 -0.701311 -1.208835
0.80 0.80 -1.119329 -0.951205 -1.584232
0.85 0.85 -1.338832 -1.221626 -1.777960
0.90 0.90 -1.632917 -0.654325 -1.274208
DML CVaR pointwise upper DML CVaR joint lower DML CVaR joint upper
0.10 -0.090125 -0.666174 -0.013869
0.15 -0.087605 -0.610999 -0.018319
0.20 -0.051828 -0.571730 0.016995
0.25 -0.154128 -0.768076 -0.072855
0.30 -0.183302 -0.735766 -0.110169
0.35 -0.131844 -0.805415 -0.042679
0.40 -0.251830 -0.844419 -0.173384
0.45 -0.266778 -0.827690 -0.192526
0.50 -0.199810 -0.832411 -0.116068
0.55 -0.209691 -0.837021 -0.126647
0.60 -0.184156 -0.897713 -0.089697
0.65 -0.085064 -0.961784 0.030993
0.70 -0.159907 -1.160878 -0.027401
0.75 -0.193787 -1.363705 -0.038917
0.80 -0.318179 -1.777399 -0.125012
0.85 -0.665292 -1.947724 -0.495528
0.90 -0.034441 -1.463364 0.154715 QTEで推定したCVaRをmatplotlibで視覚化します。
図12 QTEによるCVaRの推定
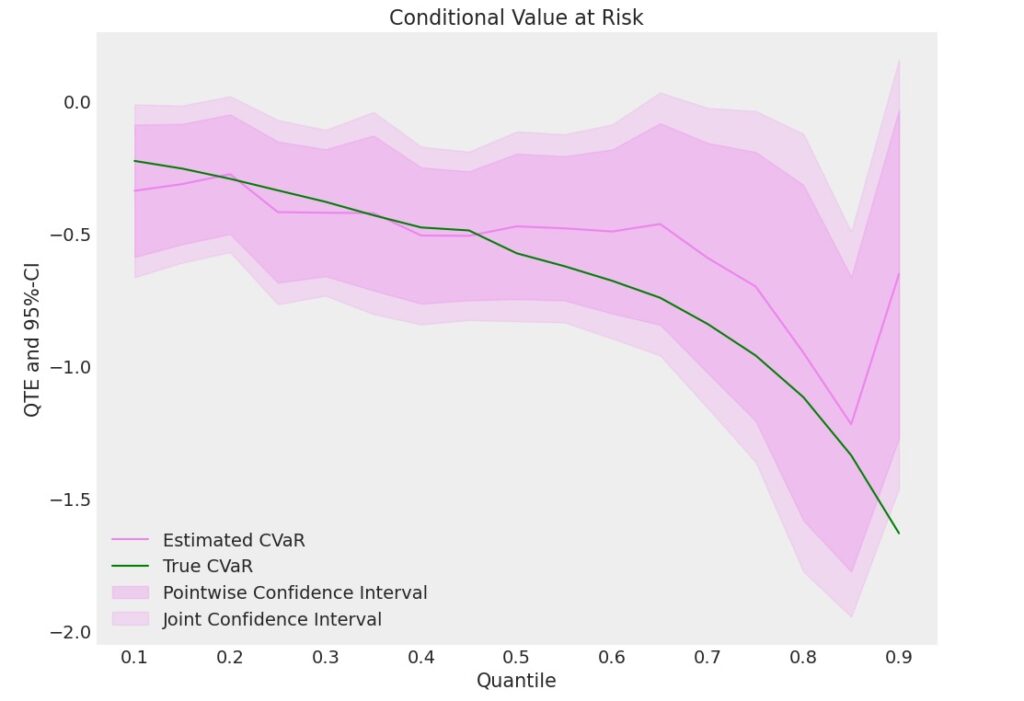
処置後のCVaRの方が小さくなっています。結果は、処置後のCVaRの推定値は、分位点が0.85以後をのぞいて、実際のCVaRに近い推定値が出力されています。
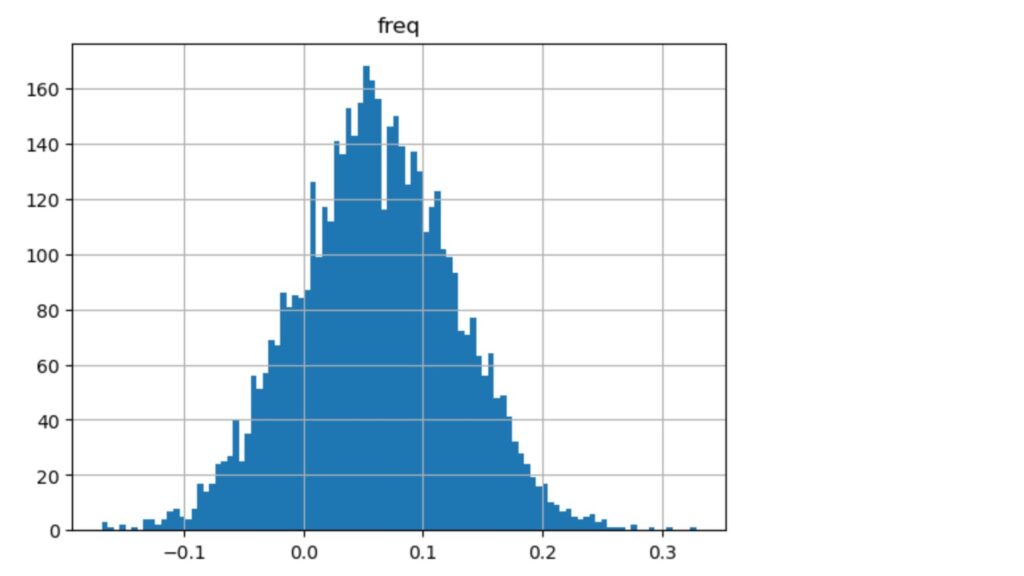
B社についてもブートストラップ法で5000サンプリングしたリターンの分布(図13、図14)を示します。
図13 ブートストラップによるリターンの分布 B社(2016/01/04~2018/01/31)
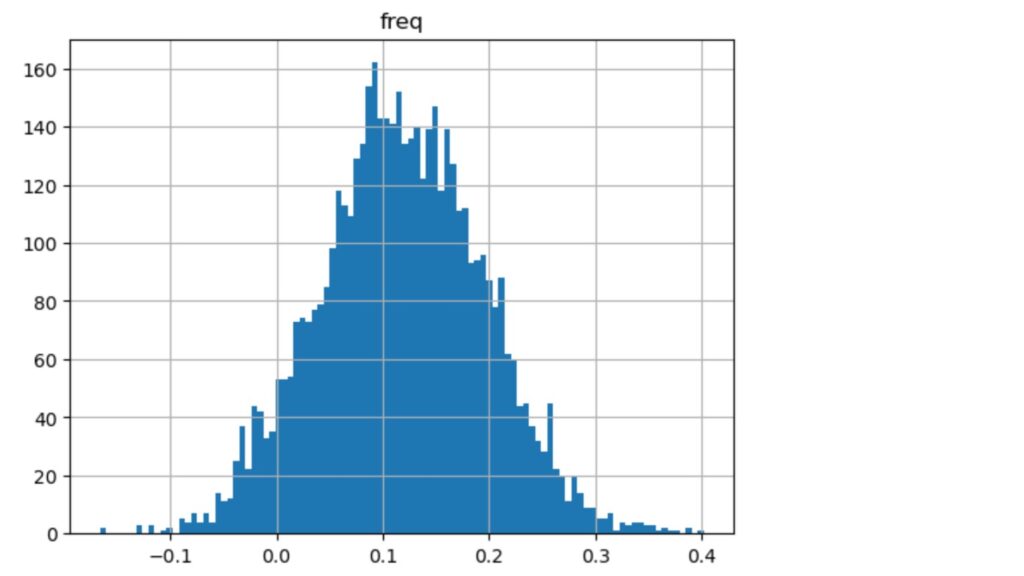
図14 ブートストラップによるリターンの分布 B社(2018/02/01~2019/12/31)
参考資料
- Robinson, P. M. Root-N-consistent semiparametric regression.
- Victor Chernozhukov, et al. Double/debiased machine learning for treatment and structural parameters.
- Nathan Kallus, et al. Localized Debiased Machine Learning: Efficient Inference on Quantile Treatment Effects and Beyond.
- Eugen F. Fama, Kenneth R. French. Multifactor Explanations of Asset Pricing Anomalies.