Statistical Consequences of Fat Tails
Real World Preasymptotics, Epistemology, and Applications
Nassim Nicholas Taleb
Statistical Consequences of Fat Tails
タレブ氏の著書は、ビジネス書と一般向けの啓蒙書の印象がありますが、本書は統計の専門書になっています。
この著書は、不確実で複雑な現実社会をどのように生きるかという、著者のIncertoプロジェクト(Antifragile,The black swan, Fooled by Randomness, The Bed of Procrustes, Skin in the Game;2001-2018)(1)~(5)の一環として執筆されています。Incertoプロジェクトの主要な考えは、現実世界の多くの不確実性の中で、不確実な情報から所与の状況でどのような行動を起こせば良いのかを理解することです。本書では、彼が”ブラックスワン”の概念と共に世に広めたファットテイルに関連した統計の性質が解説され、そのファットテイルで示す統計の現実世界における予測と認識論が展開されています。
現在の金融界が依存するリスク管理の基盤が内包する脆弱性が解説してあります。本書の非技術的概要にリストしているように、成立しない仮定の上で展開される理論の上で成立、管理されているシステムには脆弱性があります、おそらくこの内容の著書(Incertoプロジェクトの一つ)は彼以外からは出ないでしょう。金融工学が切り開いた世界の側面にある仮定の集まりの性質を詳らかにし、統計上の厚いテイルに関する技術的な適用性の問題を再認識させてくれます。
統計の基礎の章で、"ウィットゲンシュタインの定規”について触れてあります。これはテーブルを測るのに定規を使うか。定規を測るのにテーブルを使うか”という問いのことです。ことは相対的であり、結果によります。ブラックスワンは知識の不完全性の結果です。ブラックスワンが観測者に依存することを示しています。彼の比喩を使えば、”トルコ(Turkey:七面鳥)におけるブラックスワンは、肉屋の主人にとっての白鳥”です。
非技術的な概要として、彼独特のアフォリズムで、従来の金融の技術体系に対する批判が鋭利に展開されています。いくつか抜粋すると、
- "ベータやシャープレシオのような共通の乗り物の金融測度は、情報が不十分である。"
(実際、すべての経済変数と金融資産は厚いテイルである。4万銘柄の株式を調査しても薄いテイルはひとつもない。これは金融と経済の誤りの主要な根源のひとつ。厚いテイルでも平均ー分散ポートフォリオ理論が働く。)
この問題は、たとえ分散があっても、許容可能な正確さであるかどうか、私たちにはわからないことです。著者は、実際、共分散行列を使った経済論文は疑わしい、と主張しています。これは4章で詳細が論じられています。
- "ロバスト(Robust)な統計はロバストではない。実証的な分布は実証的ではない。"
(ソビエトの公式な機関紙だった、プラウダ(Pravda)という名前は、まるでジョークのような、ロシア語で”真実”を意味している。)著者は、Robustな統計は、ほとんどの専門家が気づいていない悪ふざけのようなものだと主張します。
洪水から保護するビルの建設を例にします。実証の分布は過去の最大の洪水のレベル、”過去の最大値”を示しています。
これは、 ローマの詩人、ルクレティウスによる”物の本質について”の中の誤った識別、”最も高い将来の山は、以前に見た最も高いものに等しい”という考えです。過去に起きた最大の洪水の水準を最大値に設定した場合、それを上回る水準の発生確率はゼロに設定されます。この設定に依拠すると、私たちは永遠にルクレティウスの誤りを繰り返すことになります。
この実証的な分布について、9章で、イェール大のシラー氏の論文の表紙の写しが添付されています。シラー氏はストックホルムの経済学賞を受賞されており、一般向け著書で、”根拠なき熱狂”という邦訳があります。論文のAbstractには、”過去の履歴データは、1日の株式市場の深刻な暴落の基礎になっている比率(base rate)は、相対的に低いことを示唆している”と記されてあります。
リスク管理に際し、その水準からどれくらい上の水準が保護できるかを検討する必要があります。厚いテイルにおいては、過去の最大と将来の期待最大の間の差は、薄いテイルよりずっと大きくなります。
著者らは、調査した結果、学術会で発表される経済論文の多くがこうした成立しない仮定の下で展開されている、と主張しています。
- "金融オプションのリスクは動的なヘッジによって緩和されない。"
これは、非金融界の人々には、興味のない技術的な事項かもしれない。しかし、確率のブラック・ショールズの背後にある金融ヘッジの全体の基礎と動的なヘッジの必要性、その両方に対して、誤った情報に基づいていることが、21-23章で示されます。
このように、本書はテーマ毎にファットテイルな統計の性質を数学的記述と図表を使って示してあります。11章の”ファットテイル下での確率の調整”、で展開された確率の合成と期待ペイオフ、バイナリ予測(または信用(脚注))と現実世界の連続したペイオフに関する興味深い例が示してありました。「非線形なペイオフの関数下での確率の非分離性」です。
非線形なペイオフ関数g(.)を考えてみましょう。
ランダム変数Xの変異に対する経済的、あるいは他の量的な反応は、、矛盾(discrepancy)が大きくなり、その合成はより悪化します。
確率の非分離性の数学的記述は、11.5章に示してあります。離散時間、対象期間の確率は、出来事の発生確率と出来事の平均のペイオフとの積には一致しません。
言い換えると、出来事の確率は、g(x)がHeiviside セータ関数の時だけ、予測ペイオフになります。セータはデリバティブ商品の残存期間に対する価格反応度です。
ペイオフ関数の誤解の例として以下の例があります。
2007年、ウォール街のある投資銀行は、不動産市場が下落する前に、不動産の破綻にヘッジをかける決定をしました。問題は、彼らが、破綻が何度も起こること、さらに悪いことには、そのヘッジポジションは緩やかな下落を仮定すれば利益を得ますが、大きな下落の場合、もっと大きな損失を被ることにに気づけなかったことです。彼らは危機を正しく予測しましたが、"ヘッジ"から$10bilion(100億ドル、1$:100円の場合、1兆円)の損失を被りました。
以下の図は該当金融機関がその時に保持していたヘッジです。デリバティブトレーダーの業界用語(jargon)では、"クリスマスツリー"というようです。ストライクKのプットを購入し、より低い価格(指標)のストライクK-Δ1とK-Δ2のプットを売却します。Δ2>Δ1>0です。
11.5章 図 11.5 著書で例示している金融機関のストーリーより引用して略記
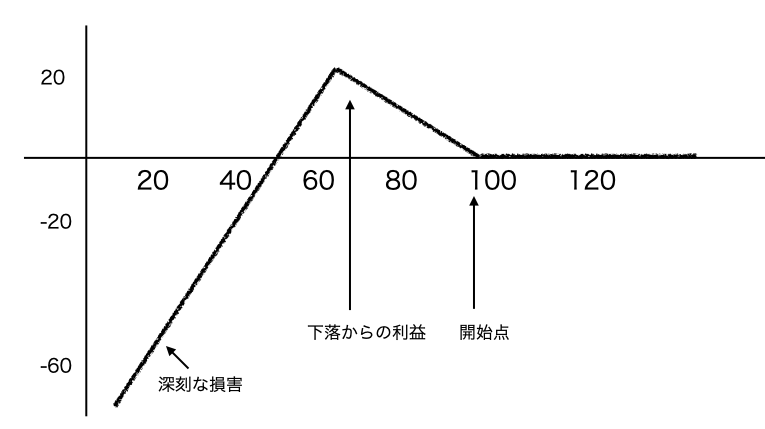
このポジションはストライクK(上の図では100以下)の緩い下落では利益を出しますが、下落幅がk-Δ1(上図、60近辺)、k-Δ2を超えると、Δ1、Δ2を超えた支払い義務が発生し、より大きな損失を負担することになります。
デリバティブの売りポジションは、投資ポジション生成時には損失額が限定されず、権利行使日に相場が変動していなければ、売りポジション生成時の売却益が利益になります。一方、権利行使日に原資産の価格がストライクKを超えていた場合、下落幅に応じた損失が発生します。
これとそっくりのCDSのポジションを以前に見たことがあります。2011〜12年の"ロンドンの鯨(London Whale)"(注2)と呼ばれた取引の件です。ペイオフ関数は期間に関して、予測ペイオフと一致しなくなり巨額な含み損を抱えることになりました。
16章では紛争に関するテイルリスクについて解説してあります。この章では不完全で信頼性の低いデータの処理に注目して、歴史的な紛争の統計的なデータを調査しています。
人類は20世紀に二つの大戦を経験しました。スティーブン・ピンカー氏は、世界が長期に渡り暴力の減少を経験し、人類の攻撃的な行動の水準の構造的な変化を指摘しています。(6)(7)しかし、データは人類の攻撃的な行動の水準の構造的な変化という考えを示していません。著者らは、紛争のデータは統計的には深刻な過小な見積もりがなされていることを発見しています。本文にデータ分析とともに著者の見解が記されてあります。一読の価値があるでしょう。
- "Fooled by Randomness." Nassim Nicolas Taleb (邦訳:まぐれ-投資家はなぜ、運を実力と勘違いするのか)
- "The Black Swan." Nassim Nicolas Taleb(邦訳:ブラックスワン-不確実性とリスクの本質)
- "The bed of procrustes." Nassim Nicolas Taleb
- "Antifragile." Nassim Nicolas Taleb(邦訳:反脆弱性-不確実な世界を生き延びる唯一の考え方)
- "Skin in the Game." Nassim Nicolas Taleb(邦訳:身銭をきれ-「リスクを生きる」人だけが知っている人生の本質)
- "The better angels of our nature." Steven pinker
- "Enlightenment Now." Steven pinker(邦訳:21世紀の啓蒙)
注2:ヘッジポジションのリバランス
この時のトレーダーのポジションは、満期日の異なる二つのCDSのポートフォリオを生成し、満期日が近い期間のCDSを購入して、満期日が遠い期間のCDSを売却するというものでした。ペイオフ関数は期間に関して、予測ペイオフと一致しなくなります。
- 2012年12月に満期を迎える期間5年のIG9を原資産のプロテクションとして購入
- 2017年12月に満期を迎える期間10年のIG9を、上のポジションのヘッジ目的でプロテクションを売却
高いイールドのプロテクションの購入と期間の長いプロテクションの売却でポートフォリオを組んでいます。
ECBは2011年12月と2012年2月に銀行システムに対して合計で€1tnの流動性供給を実施し、信用不安は後退し国債の利回りは低下して安定しました。
その後、実際に起きたのは欧州信用不安の再燃です。2012年4月に国債の利回りは再び上昇しました。
この時は、市場規模に比べて大きなポジションをとったために、CDSの市場における流動性の問題も追加されてペイオフ関数は、予測ペイオフと一致しなくなりました。
デリバティブはゼロサムです。プロテクションのポジションを取るには、それを受ける取引の相手方が必要になります。相場下落時にポジションのリバランスのために、デリバティブ商品の売りポジションを逆のポジションを新規に取ることで相殺しようとしても、流動性が低下した状況で市場に取引の受け手は見つかりません。大きな相場変動時には保持したポジションのリバランスは容易にはできません。
タレブ氏が本書の23章で記しているように、もし、誰かがオプションをオプションでヘッジするならば、オプション価格は非常に強く需要と供給に基づく価格形成になります。
連続時間のデルタヘッジングによる幾何的なブラウン運動の世界に基づくブラック・ショールズ・マートン理論(BSM)とは、非常に対照的である。BSM理論では、オプションの需要と供給は、単純にオプション価格には影響しない。誰かがオプションを購入しようとした場合、マーケットメーカーは、動的なデルタヘッジによって単純に供給することができる。
これは、危機的な状況を高める(raise):オプショントレーダーはアウト・オブ・マネーオプションの価格によって、稀な出来事の可能性(オッズ)を見積らない。それらは、まさに需要と供給によって反応する。
Statistical Consequences of Fat Tails, 23.6.2 Order Flow and Options
まさに上述の状況が、大きな相場変動時に発生し、多くのケースで巨額損失が表面化します。
他にも同時期の2011年に欧州債務危機と関連して、欧州の投資銀行でETFとオプションを使ったデルタヘッジの取引で巨額損失が表面化しています。この欧州債務危機に関連した二つのケースは、アウト・オブ・マネー オプションのポジションが、想定しない稀な出来事の発生でストライク価格を超え、需要と供給の反応によって流動性が急速に低下してヘッジができなったケースです。
流動性に関係した潜在的なリスクの問題は、さまざまなケースで表面化します。