Why Machines Learn: The Elegant Math Behind Modern AI
Anil Ananthaswamy
Why Machines Learn: The Elegant Math Behind Modern AI
本書は1950年代のローゼンブラットのパーセプトロンから現代の深層機械学習までの物語を記述してあります。
今年、2024年のノーベル物理学賞を授与された、ホップフィールド氏(John Hopfield)とヒントン氏(Geoffey Hinton)の仕事も、8章から10章に記述されています。
プリンストン大の物理学者ホップフィールドは、物理学からイジングモデルと素粒子のスピンから着想を得てホップフィールドネットワークを考案しました。
ヒントン氏については、ニューラルネットワークへの記憶の保存に関して、バックプロパゲーションによる学習方法の改善に関して一つの章を割いて詳しく記されています。彼は深層機械学習において、入力と出力層の間に隠れ層を導入しました。
甘利俊一氏も1967年に多層パーセプトロンのトレーニングに確率勾配降下法を使った技術を紹介しています。1980年代の初頭にRunmelhurt, Hinton, Williamsが深層ニューラルネットワークに対応したアルゴリズムを開発します。
Geoge Cybenkoは、 正確な種類の多層ネットワークで、十分なニューロンが与えられれば、入力を変換して必要な出力を得るどのような関数も近似できることを示しました。
各章毎に機械学習の重要な概念が誕生する経緯を、そこに至るまでの歴史から、貢献した人物たちの仕事の成果と数学的背景を丁寧に解説してあります。
7章にVapnikの仕事の成果が記されてあります。少し内容を紹介してみましょう。
データの分類に関して、ハイパープレーンはデータポイントを正確に二つの分類に分割します。フランク・ローゼンブラットのパーセプトロンを使い、もし存在すれば、そうしたハイパープレーンを見つけることができます。
ベル研にいたVapinkは、データを分類するための、パーセプトロンよりも良い方法でハイパープレーンを見つけることができる新しいアルゴリズムを考案しました。
彼の配偶者のGuyonは、80年台の初めに、パリで学生だった当時の指導者であるDreyfusに、ある論文を読むように指導されました。著者の名前はJohn Hopfieldと記されていました。論文はニューラルネットワークを構築する方法に関するものでした。それはホップフィールド・ネットワークと呼ばれるようになるメモリへ記憶するためにデザインされていました。
彼女は修士課程の研究で、ホップフィールド・ネットワークをもっと効果的にトレーニングする方法を開発しました。彼女は別のパターン認識のアルゴリズム、当時バイブルだったRichard Dudaと Peter Hurtによるパターン認識の本を取り上げました。その方法は、共同の発明者によるCovert-Hurt k-近傍アルゴリズム(k-nearest neighbor)として5章に記載されています。そしていくつかのパターン認識アルゴリズムのベンチマークと実装を始めました。Guanは博士号をとるためと、さらにベル研での仕事に対して二つのアイデアで立ち向かいました。一つは最適化マージン分類のアイデア、ホップフィールドネットワークや他のアルゴリズムを使って線形の分類を構築する場合でもWerner Krauthと Marc Mazardの仕事を認識していました。二人は1987年にホップフィールドネットワークのトレーニング法に関する論文を執筆しており、ネットワークが最小のオーバーラップでメモリを記憶する方法を示したものでした。彼らのアイデアややり方は、座標空間の二つの領域を分割するために、最適なマージンを見つけるためのアルゴリズムでした。
ベル研でBernhard BoserがGuyonにVapnikの最適化マージン分類について話したとき、1991年の秋に実装したところでした。
Vapnikは低い次元で線形に分離できないものを高い次元に持っていくように要求しました。Guyonはそうしたアイデアに博士課程で出会っていました。鍵となる論文の一つは、ロシアの研究者、M.A.Aizemanによって1964年に執筆されました。彼らの論文は物理学のアイデアにインスパイアされて、非線形の境界を見つけるためにローゼンブラットのパーセプトロンによって稼働できるアルゴリズムを開発しました。
図1

上の図1では、三角形から円の境界を定める(分割するための)直線、または線形に分割するハイパープレーン、を引く方法はありません。しかし、これらのデータを(下の図2のように)三角形が円の上部に置けるような三次元の中に置く案があれば、私たちはそのような分割するハイパープレーンを見つけることができます。
図2
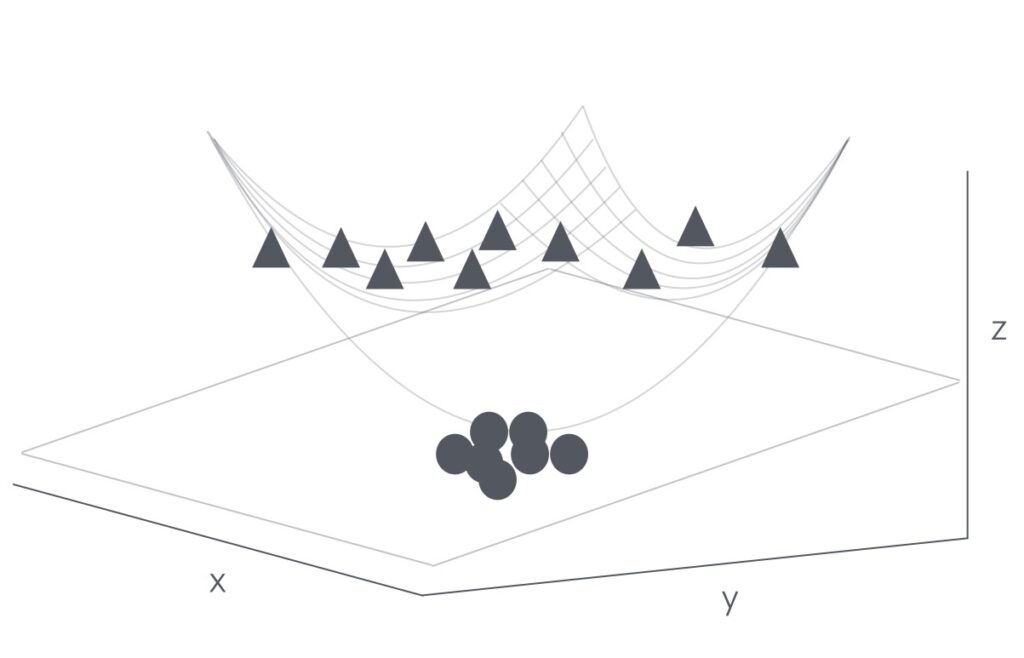
アルゴリズムは同時に二つのことを実行する必要があります。
- データが何らかの高い次元の空間にマップできるように新しい特徴を作る。
- 新しい空間上に点乗積(dot積)の実行を避けて、分割するハイパープレーンを見つけることができる。
Aizerman, Braverman, Rozonoerは、1964年の論文にパーセプトロンのアルゴリズムのために実行するための方法を示していました。
約10年後、よりわかりやすいものとして、彼らは開発されたマッピングの方法を使いました。三つの特徴を使って、二次元データを三次元データにマップすることを始めます。
もし、私たちが二つの低次元ベクターを関数Kに入れるなら、その関数は、より高い次元の空間の引数ベクターのドット積に等しい値を出力します。
K(a,b) = φ(a) φ(b)この関数Kはカーネル関数と呼ばれます。
ある高次の空間での点乗積(dot products)を計算するためにカーネル関数を使う方法は、カーネルトリックと呼ばれます。
私たちはカーネル化したパーセプトロンアルゴリズムを見ることができます。
各データポイントは3次元にマップされ、その時、パーセプトロン・アルゴリズムは線形に分割するハイパープレーンを見つけるために使うことができます。図3を参照してください。
図3
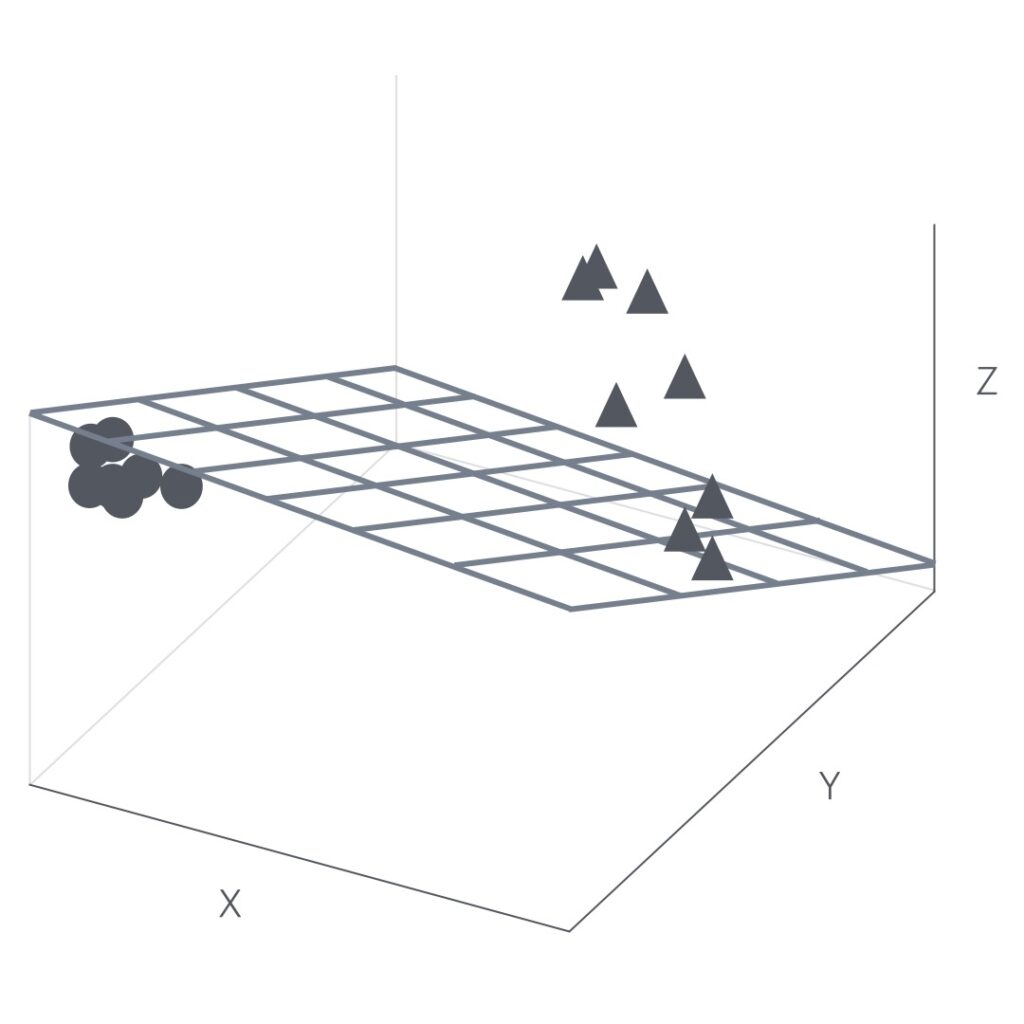
3角形から円を分離するプレーンを見つけるアルゴリズムによって、 3D空間で2種類のデータポイントが明確に分離されているのを見ることができます。
どのような新しい二次元のデータポイントが与えられても、私たちはそれを3D空間にマップすることができ、ハイパープレーンへの相対的なその位置に依存して、3角形または円として分類することができます。
この3D空間の輪郭を元の2次元空間に戻すことで、3角形から円を分離する非線形の境界を取得します。
Guyonは彼女の博士論文の時にカーネルの周辺で研究しており、仕事に着いた後もそうしました。特に彼女は、1975年のMITのコンピュータ・ニューロサイエンスのTomaso Poggioによって紹介された多項式カーネル(Polynomial kernel)と呼ばれる種類のものを使っていました。
以下に多項カーネルの一般的な様式を示します。
K(x,y) = (c + x・y) **d c,d は定数定数のc,d にそれぞれ 0, 2を設定すると、パーセプトロン・アルゴリズムで使っていた以下の式を得ます。
K(x,y) = (x・y)2彼女は、パーセプトロンアルゴリズムのように、高次元でそれらの魔法を実行するのにカーネルトリックを使うことができました。
それは、新しい特徴を作ることによってデータを高次におく、そして高次の空間で最適化マージンの分類を構築するというVapnikのアイデアを、彼女の夫が彼女に語る時、1991年まで待たなければならなりませんでした。
これらの特徴は、個別の特徴を乗算することによって生成することができました。例えば、
xj -> φ(Xj)Vapnikはこの方法で新しい特徴を作ることによって、アルゴリズムを実装するために、Bernhard Boserが必要でした。
Boserが職場でGyuonにこれを話した時、彼女はすぐにそうしたアルゴリズムは無用だとわかりました。彼女はBoserにそれらの特徴の生成物を作る必要はないと言いました。彼女は提案しました。"カーネルトリックを使いましょう。"
彼女はトリックを夫に説明し、すぐにVapnikの最適化マージンアルゴリズムをカーネルを使ったものに書き直しました。
こうしたカーネル関数の中にRBFカーネルがあります。
RBFカーネルは、アルゴリズムが、何らかの大きな次元の空間で線形に分離可能なハイパープレーンを常に見つけるのを助けることができます。それがどのれほど複雑であっても、低次の空間へマップするとき、どのような決定境界も見つけることができます。すべての関数の近似であると言えます。このフレーズを気に留めておいてください。本書では、全体の章を通して、どのような確かな種類の人工のニューラルネトワークもまた、全体の関数の近似になるということを議論し、そのときに、十分なニューロンが与えられれば、それらはどのような問題を解くこともできるということに、全体の章を充てています。
1964年のVapnikの最適化マージン分類とカーネルトリックの組み合わせは、信じられないほど強力であることを立証しました。
VapnikとCortesは彼らのアルゴリズムをサポートベクターネットワークと呼びました。ドイツのコンピュータ・サイエンティストで、現在マックスプランク研究所でインテリジェント・システムのディレクターであるのBernhard Scholkopfは、ニューラルネットワークからアルゴリズムを区別するために、"サポートベクターマシーン"(SVM)に名称変更しました。
SVMは現在、ゲノム解析、癌の研究、ニューロロジー、画像診断、HIV薬のカクテルの最適化まで、気候調査、地球物理学、宇宙物理学の広範囲な応用分野の発見に使用されています。
80年代はニューラルネットワークが機械学習を支配していました。そして、90年代になって、突然、皆がカーネル法に切り替えました。
現在、ニューラルネットワークが再び、現代の機械学習を支配しています。本質的に、理論的な前進は、ニューラルネッットワーク・サービスとカーネルマシンの間の期待を掻き立てるリンクを見せ初めています。
ヒントン氏らは、ニューラルネットに隠れ層を導入して、バックプロパゲーションによる多層ニューラルネットワークの学習能力を向上させることに焦点を当てていました。
図1の例で見たデータを分類するのに、SVMでは、カーネルをデザインする必要がありました。しかし、十分なニューロンのあるニューラルネットでは、私たちがしなければならないことは、X1,X2の入力とデータを正しく分類するために必要となる特徴をネットワークに理解させることです。
隠れ層の三つのニューロンのニューラルネットワークで、以下の(図3)決定領域を見つけられるでしょう(もっと深い隠れ層があれば、より滑らかな決定境界にすることができます)
図4

トロントのヒントン氏の元にいたLeCun氏がニュージャージーのベル研にわたりました。彼はベル研で合衆国の郵便サービス(USPS)から大量の手書き数字コードの画像のデータセットにアクセスすることができました。USPSはZIPコードを認識する処理に興味があリました。LeCunは手書きの数字を認識するためにニューラルネットを使いました。彼のCNNを使ったアルゴリズムは、LispからC言語を経由してDSP上に実装され、手書きのZIPコードの認識に使用されました。顧客向けのシステムのため、パターン認識のCNNのソフトウエアはオープンソースにはなりませんでした。
LeCunのLeNetは、銀行業界で数字の読み込みと認識に使用されました。これはバックプロパゲーションによる深層学習を使った実際の応用例の一つになりました。
ヒントン氏のチーム(Krizhevsky, Sutskever, Hinton)がGPUにCNNを組み込んで(AlexNet)画像認識でSVMを超える成果をあげました。彼らのチームを中心にGPUに実装したニューラルネットが使われるようになって、隠れ層を深くしたディープ・ニューラルネットが様々な分野で成果を上げるようになりました。
そして、現在のTransformerを使った自然言語処理が展開されていきます。LLMは言語の構造を学習し、自動学習画像処理ネットワークは画像の統計的な構造を学習します。
本書のサブタイトルにあるように、パーセプトロンから始まり、現在のAIの技術まで、トピック毎に開発者たちの仕事を通じて、技術の背後にあるエレガントな数学が解説されています。現在までの技術の推移を把握できる内容になっています。