gCastleに実装された探索アルゴリズムの中で、強化学習を使ったアルゴリズムが高い性能を示しています。本稿ではこの探索のための強化学習アルゴリズムを解説します。
強化学習を使った探索
強化学習は一般的にポリシーを学習することを目的に用いられますが、彼らはこれをDAGの探索に使っています。
巡回セールスマンの問題と同様に、d次元のnシーケンスでベストスコアを導くことで、入力データからバイナリの隣接行列の生成を考えます。
隣接行列を出力するためにエンコーダ/デコーダ・モデルを作りますが、エンコーダ自己アテンションモデルを元にしたトランスフォーマー・アーキテクチャを使っています。これが、このアルゴリズムの特徴です。
LLMや画像の生成AIは、トークンの結びつきを発見することができるトランスフォーマー・アーキテクチャを元にしています。彼らが提案しているアルゴリズムは、データ間の関係の強さを学習することで因果探索でトランスフォーマー・アーキテクチャが有効なことを示しています。
RLアルゴリズム
彼らは、RLを探索の戦略としてベストスコアのDAGを探索するために用い、最終的にグラフを出力します。すべてのグラフはトレーニングの間に生成され、ベストのrewardを格納します。
よく知られたスコア関数、BIC, MDL, BGe, などがありますが、一般的にNP-hardの問題があります。
非周期の組み合わせによるDAGの数は、グラフノードの数によって指数的に増加します。この問題に対処するために、最も多いのが、例えば、GES(Greedy Equivalence Search)のように局所的なヒューリスティックスに依拠するアプローチです。
max-min hill climbing法というハイブリッドなアプローチがあります。これは、スコアを基にした方法を適用する前に、探索空間を減らすために制限を基にしたアプローチを取ります。しかし、この方法は、問題に応じたスコア関数と探索ストラテジーの組み合わせを選択する基本的な方法が、一般的に不足しています。(以下のブログでRのライブラリpcalgでグラフィカルモデルによる因果推論としてhill climbingアルゴリズムを使った因果探索とグラフの生成例を示しています。)
モデルは観測データを入力として、rewardを計算することでグラフ隣接行列を生成します。
Rewardはあらかじめ定義したスコア関数と、非周期の二つのペナルティ項の組み合わせです。
彼らが提案するBICスコアを使ったアプローチは、LiNGAMで使っているものと同じスコア関数GES(Greedy Equivalence Search)の性能を上回ります。
AlphaGoに見られるように、多くのRL(強化学習)アプリケーションの成功例があります。RLの理論的な枠組みは、自然に探索のタスクを含むことができることです。彼らのこのアルゴリズムに関するアプローチでは、actor(エンコーダ/デコーダモデル)とRewardの設計に違いがあります。Rewardは、非周期の制限とスコア関数の組み合わせによる因果探索のために特別に設計されています。
モデルの定義(Actor-Critic)
データ生成手続きのために、以下のモデルを仮定します。
d-ノードの DAG gにおいて、各変数xiはノードiに関連づけられており、xiの観測値は、グラフ内の親の関数に独立したノイズ成分 niを付加したものとして得られます。
xi = fi(Xpa(i)) + ni, i = 1,2,...,dここで、Xpa(i)は、グラフの中でxj からxi へのエッジがあるような変数xi のセットで示され、ノイズniは、結合して独立したものとして仮定されます。
入力データセットは、X={xk}k=1 m で与えます。xkは k番目の観測データのサンプルを示します。彼らは、観測データから因果グラフを推論するために、ニューラル・ネットワークを使います。観測データを入力、グラフ隣接行列を出力としたニューラルネットワークを元にしたグラフ生成処理を設計するのが目的です。
巡回セールスマン問題に着想を得て、n次元のd都市の巡回シーケンスを表します。彼らは、一致するグラフが、非周期でベストスコアを持つように、バイナリの隣接行列の生成を考えます。これは、グラフ生成のためのエンコーダ/デコーダを考えることです。
図1 スコアを元にした因果探索のための強化学習(参考資料1より引用して略記)
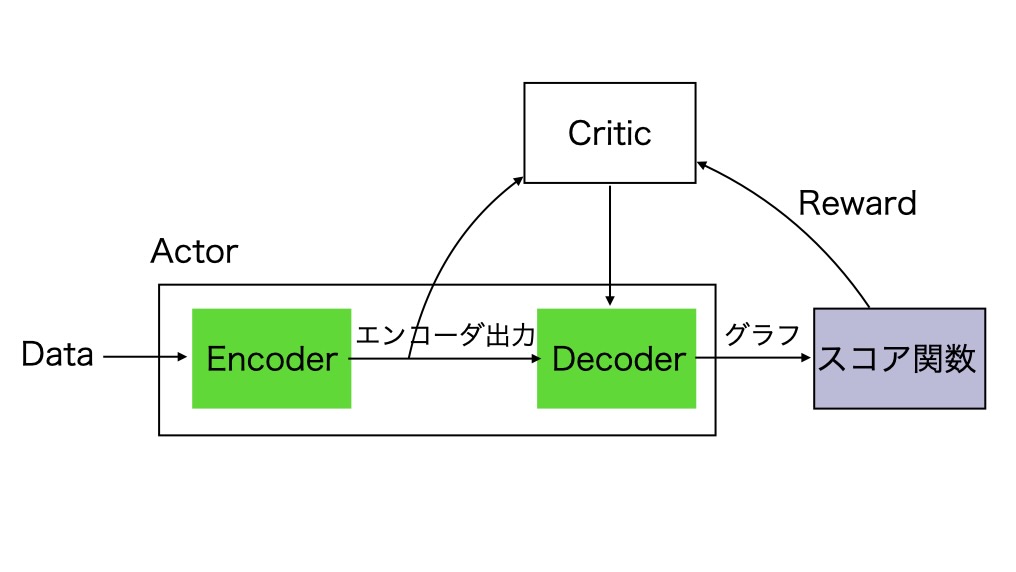
- エンコーダ
トランスフォーマー構造のアテンションを元にしたエンコーダを使います。2017年にGoogle社のVaswani氏らによって提案されたアーキテクチャです。Chat GPTやLlamaなどのLLMの基礎になっているものです。
構造化DAGの制限を伴う自己アテンション・モデルの方法は、変数の間の因果関係を発見することができます。自己アテンションは、以下の図2で示すように出力の全てが次のすべての入力に接続されているネットワークです。1
図2 自己アテンション・モデル
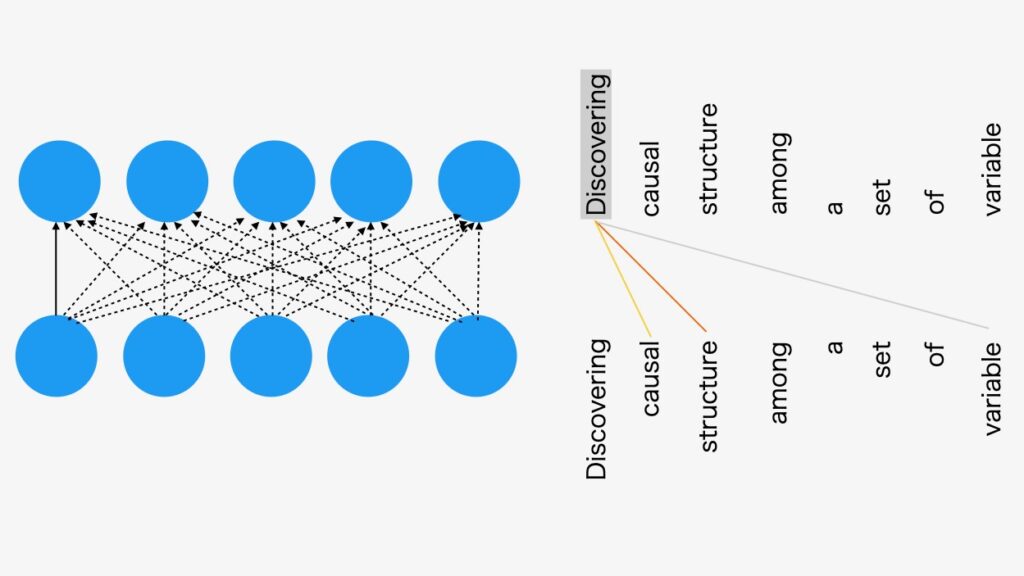
自己アテンション・モデルは、すべての出力がすべての入力に接続されます。例えば、与えられた入力トークンのシーケンスは、自己アテンションは同じサイズの出力シーケンスを出力することができます。
図2の例は、言語モデルのトークン入力です。ここで解説している因果探索アルゴリズムでは、入力は、任意の観測データセットになります。(関数IIDSimulation()の出力としてのテストデータセット)
トランスフォーマーのマルチヘッド・アテンションの構造を、図3に示します。
図3 マルチヘッド・アテンション
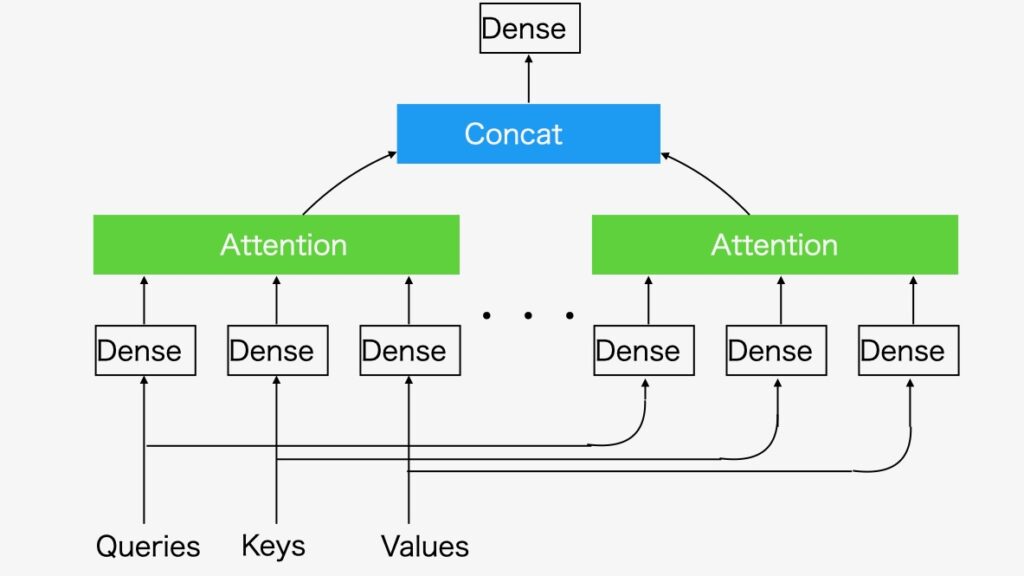
生成AIは、アテンション・モデルによって、データ間の関係性と構造を把握し、目的のデータの塊を生成します。
このRLの仕組みを活用してDAGを出力しています。
- デコーダ
デコーダは、二つのエンコーダの出力enci enc jの間の関係を構築することによってグラフ隣接行列を出力します。彼らは、以下の単一層のデコーダーを考えます。
gij(W1,W2,u) = uT tanh(W1 enci + W2 encj)ここで、W1,W2⊂ R dh x de, u ⊂ R dh x 1 は、訓練の変数で dh は、デコーダーに関連した隠れた次元です。バイナリの隣接行列を生成するために、各エントリーgijをロジスティック・シグモイド関数δ(・)に渡します(図4)。それからxiからxjへのエッジの存在確率を示す確率σ(gij)を、ベルヌーイ確率分布によりサンプルします。自己ループを避けるために、隣接行列の(i,i)番目のエントリーをマスクします。
図4 シグモイド関数σ(・)
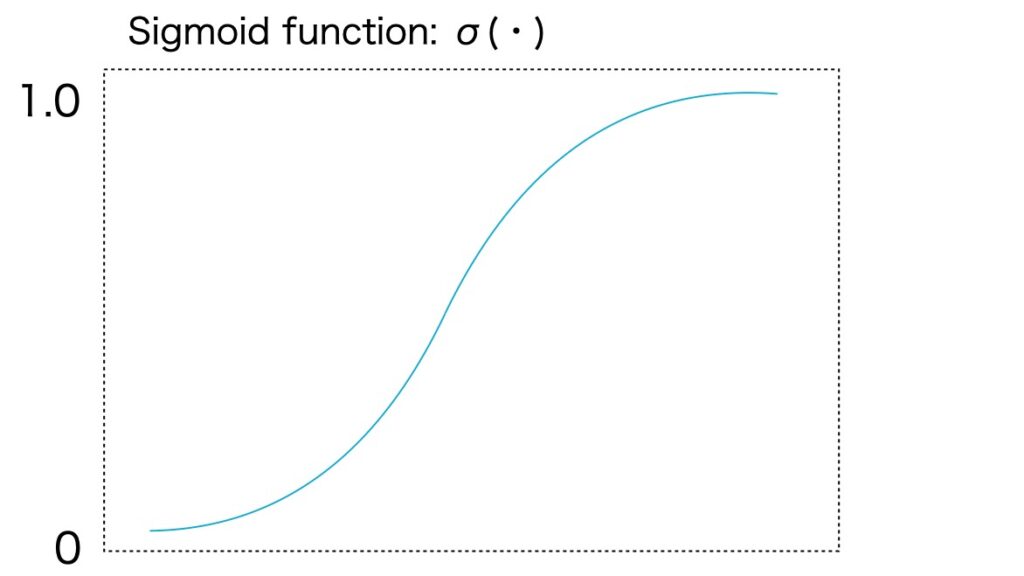
シグモイド(ロジスティック)関数
σ(a) = (1 + e -a) -1彼らのエンコーダ/デコーダ モデルには、いくつかのデコーダーの選択肢がありますが、彼らは、単一層のデコーダが最良であることを発見しています。彼らの論文(参考資料1)のAppendixに、デコーダーの比較が掲載されています。
探索用の強化学習
- スコア関数
スコア関数にはBICを使います。与えられた有向グラフに関するBICスコアは、
Sbic (g)= -2 log p( X; θ^, g ) + dθ log m,θ^:最大尤度estimator, dθ:パラメータθの次元を示します。
彼らは、iid ガウシアン加法ノイズを仮定します。各因果関係に線形のモデルを適用するならば、x^ik を、k番目の観測サンプルのi番目のエントリー、xikに対応するestimatorとします。そこでBICスコアを
Sbic(g) = Σi=1d (m log(RSSi /m)) + #(edges) log mΣi RSSi は、NOTEARSで使用されている最小自乗ロスです。線形のモデルの仮定で、他の回帰法をxikを推定するために使うことができます。
- 非周期性
残りの問題は非周期性の制限です。暗黙の制限として、非周期性を強制するために、スコア関数に非周期のペナルティ項を追加します。
バイナリの隣接行列Aの有向グラフは、以下の(*)を満たすときにだけ非周期です。(注1)
h(A) := trace(eA) - d = 0 --------(*)ここで、eAは Aの exponentialです。
- Reward
Rewardは、スコア関数と非周期性の制限との組み合わせです。
reward:= -[S(g) +λ1 I (g ⊂DAGs) + λ2 h (A)]ここで λ1、λ2>0 はペナルティ変数。
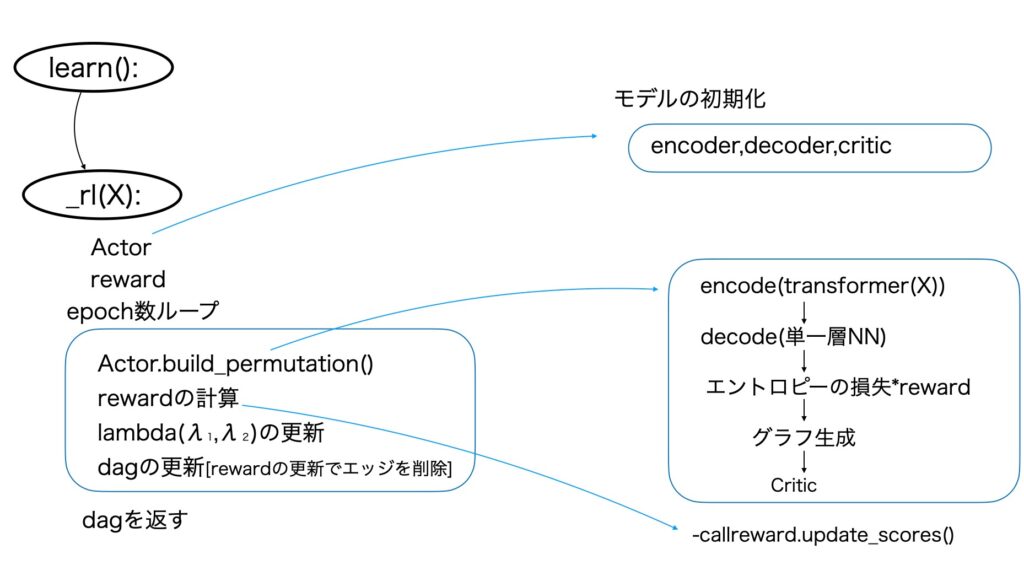
強化学習で因果の構造を学習します。処理の概要を以下の図5に示します。
図5 強化学習による探索処理の概要
DAGの出力
ベストスコアのDAGに注目しているため、トレーニング過程の間に生成されたすべてのグラフを記録します。最良のrewardの一つを出力します。
以下のブログにサンプルで示したように、テストプログラムではrlアルゴリズムの出力結果は、元のDAGを再現しています。
図6 RL(Actor-Critic)アルゴリズムで探索したグラフ隣接行列(左)と元のグラフ隣接行列(右)
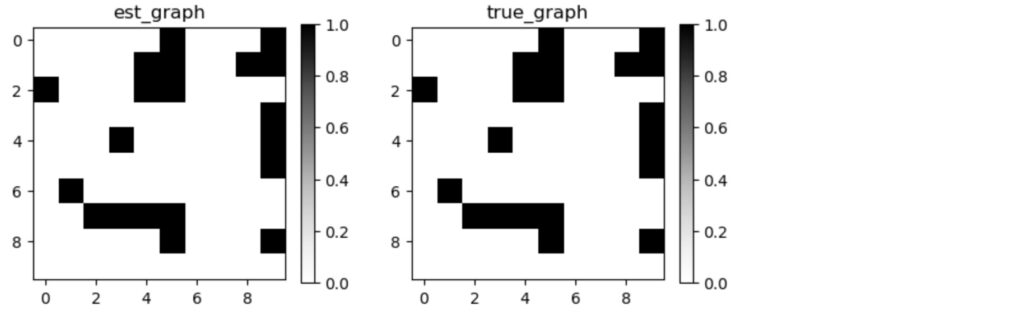
RLを用いた因果探索アルゴリズムは、非常に良い結果を生成します。
しかし、このアルゴリズムは、ノードの数が30を超えると性能が低下してきます。このスケールの問題を改善しているのがNORLアルゴリズムです。RL同様にgCastleに実装されています。
参考資料
- Shengyu Zhu, et al. Causal Discovery with Reinforcement Learning.
- Shengyu Zhu, et al. Ordering-Based Causal Discovery with Reinforcement Learning.
- X.Zheng ,et al. DAGs with NO TEARS: Continuous optimization for structure learning.
- 他のアテンションを元にしたモデルに、Velickovic et al. (2018)のグラフ・アテンション・ネットワーク(GAT)があります。
Velickovic et al. GRAPH ATTENTION NETWORKS ↩︎