causal-learnによる因果探索

　【マネーサプライと物価上昇の因果推論】で、二つの時系列データ間のGranger因果性を調べました。ベクター自己回帰モデル(Vector Auto-Regression:VAR)を適用したものです。他にも、近年、新しい因果推論、因果探索アルゴリズムが提案されています。PythonやR上に実装された因果推論パッケージがAI関連技術に投資している企業や機関からリリースされています。

　causalQueries, causalml, causal-learn等、【為替レートと地政学的リスク-割り込まれた時系列データのCausalPyによる分析】で用いたCausalPyもその一つです。

　ここでは、その中でPythonベースのcausal-learnに実装された因果探索アルゴリズムをいくつか評価します。causal-learnは因果関係を理解するための因果探索だけでなく、条件独立性テストのアルゴリズムが実装されています。

causal-learnの因果探索アルゴリズム

　多くの因果探索メソッドは観測データをもとに、そのデータから推定する目的で、固定の因果モデルを仮定しています。古典的な因果探索のアプローチは二つに大別されます。

　一つは条件独立性を基礎にした因果構造のマルコフ同値類を推定するものです。結果として同じ条件独立性を示すDAGを表示します。データ内の静的に独立した属性と基礎となる因果構造のd-separation属性の間で一致するものを仮定します。これはスコアをもとにしたアプローチと呼ばれます。BIC(Bayesian Information Criterion)などのスコアで最も高い同値類を探します。

　この因果モデルとしてcausal-learnに実装されているPC(Peter-Clark), 高速因果推論: FCI(Fast Causal Inference), CD-NOD(Constraint-based causal Discovery from heterogeneous/NOnstationary Data)を評価します。

　もう一方のアプローチとして、抑制関数因果モデル、直接の原因とともに独立したノイズ項のある関数として結果を示します。抑制関数因果モデルによって示される因果の方向が、一般的に識別されます。

　線形非ガウシアン非周期モデル（LiNGAM), 加法的ノイズモデル、事後非線形因果モデルがあります。これらのアルゴリズムは、causal-learnではP-値を出力する関数として実装されています。

　現実のデータセットを使って、これらの実装を評価してみましょう。

　該当データセットに対して、これらの因果探索アルゴリズムで因果関係を調べます。ツールの開発サイトでは、テストデータを生成して評価しています。以下のGitで参照できます。

https://github.com/py-why/causal-learn/

　ここでは、市場に関係するデータとして、以前ポストした"マネーサプライと物価上昇の因果推論"で用いたデータセット(過去２０年間の為替レートとCPIの月次データ)を使います。

causal-learnのインストール

　ツールの実行環境として、以下のライブラリが必要になります。

numpy　
networkx
pandas
scipy
scikit-learn
statsmodels
pydot

　インストールにはpipを使います。

pip install causal-learn

(base) nostname:~ username$ pip install causal-learn
Collecting causal-learn
  Downloading causal_learn-0.1.3.8-py3-none-any.whl (174 kB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 174.5/174.5 kB 915.5 kB/s eta 0:00:00
Collecting pydot
  Downloading pydot-2.0.0-py3-none-any.whl (22 kB)
Requirement already satisfied: pandas in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (1.5.3)
Requirement already satisfied: matplotlib in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (3.7.0)
Requirement already satisfied: statsmodels in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (0.13.5)
Requirement already satisfied: tqdm in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (4.64.1)
Requirement already satisfied: graphviz in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (0.20.1)
Requirement already satisfied: networkx in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (2.8.4)
Requirement already satisfied: scipy in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (1.10.0)
Requirement already satisfied: numpy in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (1.22.3)
Requirement already satisfied: scikit-learn in ./anaconda3/lib/python3.10/site-packages (from causal-learn) (1.2.2)
Requirement already satisfied: cycler>=0.10 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (0.11.0)
Requirement already satisfied: python-dateutil>=2.7 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (2.8.2)
Requirement already satisfied: kiwisolver>=1.0.1 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (1.4.4)
Requirement already satisfied: pillow>=6.2.0 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (9.4.0)
Requirement already satisfied: packaging>=20.0 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (22.0)
Requirement already satisfied: fonttools>=4.22.0 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (4.25.0)
Requirement already satisfied: pyparsing>=2.3.1 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (3.0.9)
Requirement already satisfied: contourpy>=1.0.1 in ./anaconda3/lib/python3.10/site-packages (from matplotlib->causal-learn) (1.0.5)
Requirement already satisfied: pytz>=2020.1 in ./anaconda3/lib/python3.10/site-packages (from pandas->causal-learn) (2022.7)
Requirement already satisfied: threadpoolctl>=2.0.0 in ./anaconda3/lib/python3.10/site-packages (from scikit-learn->causal-learn) (2.2.0)
Requirement already satisfied: joblib>=1.1.1 in ./anaconda3/lib/python3.10/site-packages (from scikit-learn->causal-learn) (1.1.1)
Requirement already satisfied: patsy>=0.5.2 in ./anaconda3/lib/python3.10/site-packages (from statsmodels->causal-learn) (0.5.3)
Requirement already satisfied: six in ./anaconda3/lib/python3.10/site-packages (from patsy>=0.5.2->statsmodels->causal-learn) (1.16.0)
Installing collected packages: pydot, causal-learn
Successfully installed causal-learn-0.1.3.8 pydot-2.0.0
(base) hostname:~ username$

データの準備

　評価用に、以下のブログポストで用いたCPIのデータを使います。

: マネーサプライと物価上昇の因果推論
「流動性の罠　再考」で示したようにマネタリーベースの増加が期待物価上昇率に影響する経路はあるのでしょうか。消費者物価(CPI)の過去２０年間のデータに注目すると、ドル円為替レートと連動して推移している ...

import sys
import pandas as pd
import numpy as np

urlpath = "./ファイルパス/cpifx5.csv"
df_cpi = pd.read_csv(urlpath,index_col=0)
df = pd.DataFrame({'x':df_cpi['Usdjpy-pct-cum'], 'y':df_cpi['Cpi-pctchg-cum']})
data = df.to_numpy()
df_x =  pd.DataFrame({'x':df_cpi['Usdjpy-pct-cum']})
df_y =  pd.DataFrame({'y':df_cpi['Cpi-pctchg-cum']})
data_x = df_x.to_numpy()
data_y = df_y.to_numpy()

　df_cpiのデータフレームは以下のようになっています。

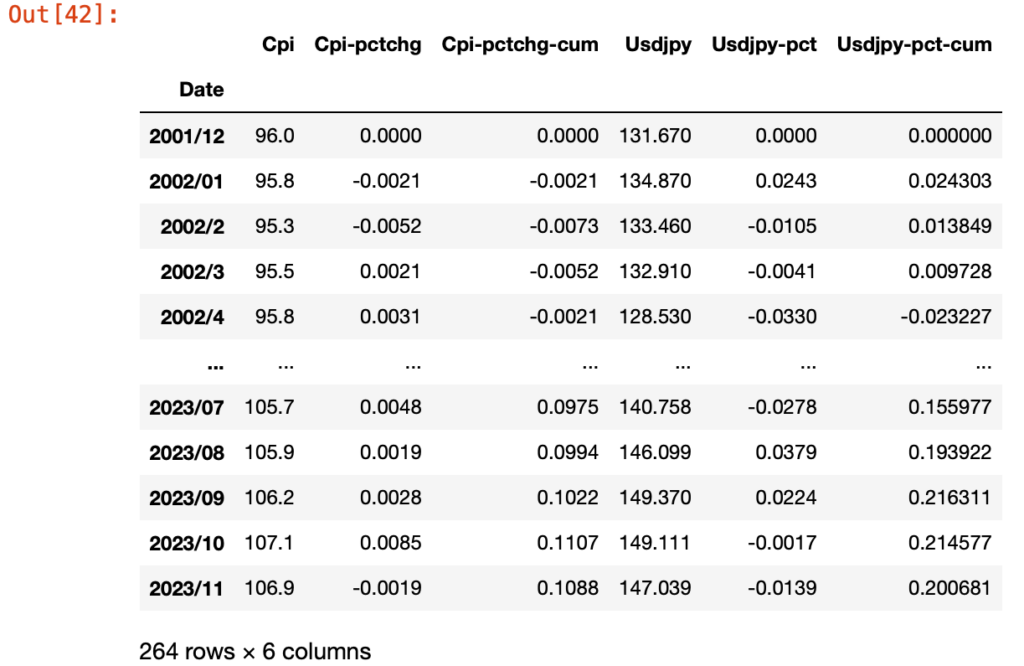
　dataは次に示すようにnumpyの二次元配列になります。

array([[ 0.00000000e+00,  0.00000000e+00],
       [ 2.43031822e-02, -2.10000000e-03],
       [ 1.38486704e-02, -7.30000000e-03],
       [ 9.72758548e-03, -5.20000000e-03],
       [-2.32270455e-02, -2.10000000e-03],
       [-5.80049183e-02,  1.10000000e-03],
       [-9.46001142e-02,  0.00000000e+00],
       [-9.24247461e-02, -4.10000000e-03],
       [-9.97715486e-02, -1.00000000e-03],
       [-7.51289918e-02, -1.00000000e-03],
       [-7.00399333e-02, -3.10000000e-03],
       [-6.94682714e-02, -3.10000000e-03],
       [-1.00646854e-01, -3.10000000e-03],
       [-9.04530886e-02, -6.20000000e-03],
...

Peter-Clark(PC)アルゴリズム

　ピーターとクラークによって提案されたアルゴリズムです。以下の文献⁽¹⁾にアルゴリズムが解説されています。

(1) Spirtes, P., Glymour, C. N., Scheines, R., & Heckerman, D. (2000). Causation, prediction, and search. MIT press.

　causal-learnに実装されたAPIを使った例を示します。因果の構造はDAGによって示されます。

from causallearn.search.ConstraintBased.PC import pc
# default parameters
cg = pc(data)

# or customized parameters
#cg = pc(data, alpha, indep_test, stable, uc_rule, uc_priority, mvpc, correction_name, background_knowledge, verbose, show_progress)

# visualization using pydot
cg.draw_pydot_graph(labels=['usdjpy', 'cpi'])

# or save the graph
from causallearn.utils.GraphUtils import GraphUtils

pyd = GraphUtils.to_pydot(cg.G)
pyd.write_png('test1.png')

　以下の図が出力されます。出力された図は推定された因果のスケルトン（causal skeleton）です。

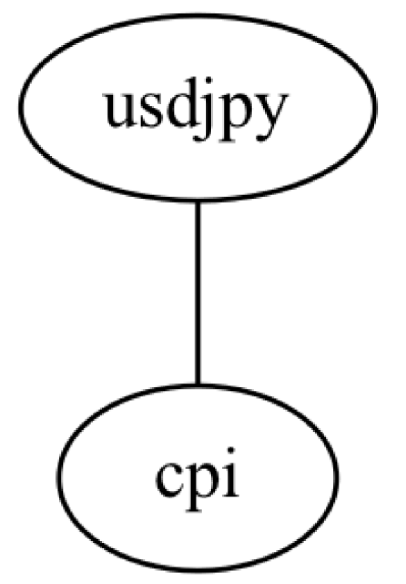
図１　因果スケルトン

　因果の構造である両者の関係として、どちらかに原因と結果を示す方向性がありますが、データから解析した出力はスケルトン（骨組み）の関係だけが示されます。因果の方向性までは特定されません。

高速因果推論(Fast Causal Inference)

　FCIアルゴリズムは以下の論文⁽²⁾で解説されています。

(2) Spirtes, P., Meek, C., & Richardson, T. (1995, August). Causal inference in the presence of latent variables and selection bias. In Proceedings of the Eleventh conference on Uncertainty in artificial intelligence (pp. 499-506).

　テストコードを示します。

from causallearn.search.ConstraintBased.FCI import fci

# default parameters
g, edges = fci(data)

# or customized parameters
#g, edges = fci(data, independence_test_method, alpha, depth,
#max_path_length,verbose, background_knowledge, cache_variables_map)


# visualization
from causallearn.utils.GraphUtils import GraphUtils

pdy = GraphUtils.to_pydot(g)
pdy.write_png('test2.png')

　以下の図が出力されます。

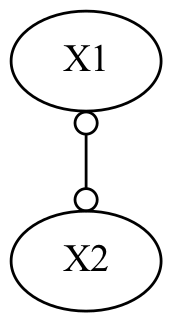
図２　出力PAG

　関数API fci()の戻り値のgは、GeneralGraphオブジェクトです。g,graphは　PAGで、終端ノードの表示は、以下のようになります。

図3　fci()の戻り値　(G = g.grapchを示す）

　図２の出力では、X1,X2の間にはd-separates（d-separationはグラフで定義⁽³⁾）がセットされません。これは、A(X1)とB(X2)の間に誘発する経路(原因)はあるが、その原因となる経路の方向性がないことを示しています。両端に終端のある不完全な指向性の誘発経路グラフです。AとBにはPOIPG(partially oriented inducing path graph：不完全な方向性の経路グラフ)内で隣接し、それは、AとBの間に誘発経路があることを意味し、終端の"o"は、その経路の方向性を判断できないことを意味しています。

　APIにデフォルトの設定値を与えた、データ系列のみの情報では因果の方向性が規定できませんが、background_knowledgeという引数で、APIに事前情報を与えることができます。PCアルゴリズム、CD-NODも同様にbackground_knowledgeを与えることができます。引数のパラメータ指定はcausal-learnのgitを参照してください。

(3) S. Lauritzen.(1996) Graphical Models. Oxford University Press .

CD-NOD

　CD-NODは、(Constraint-based causal Discovery from heterogeneous/NOnstationary Data)の略です。

　観測されない変数因子として交絡因子を想定した因果探索にPeter-Clark (PC)アルゴリズムを実行します。

　CD-NODを因果探索として提案した論文⁽⁴⁾には、現実世界のデータとして香港株式市場の株式と米国株式市場の日次リターンに適用した例がアルゴリズムの検証に用いられています。

　ここでは株式間での因果の構造を推定し、因果メカニズムを持つ株式のリターンを推定しています。下の図は、参考資料(3)の図１５を引用して略記したものです。HKEX 香港株式市場の主要10銘柄の日次リターンのデータにCD-NODを適用しています。

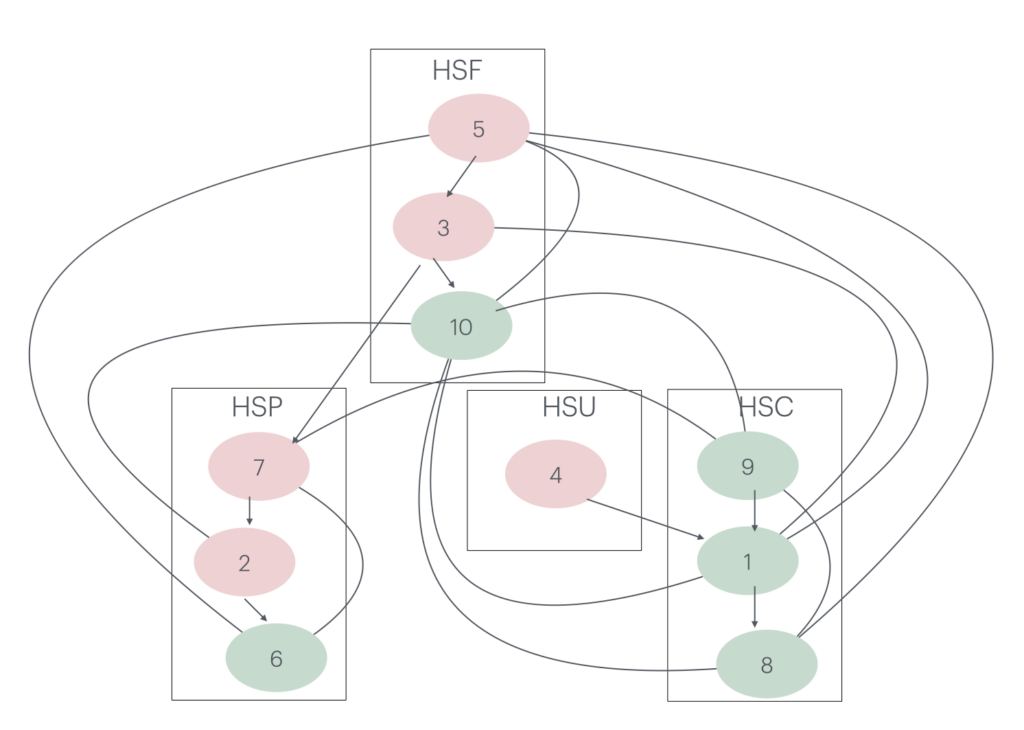
1-10の各株式は以下のサブインデックスに含まれます。
HSF:Hang Seng Finance Sub-index
HSC:Hang Seng Commerce & Industry Sub-index
HSP:Hang Seng Properties Sub-index
HSU:Hang Seng Utilities Sub-index

図4　HK主要10銘柄の因果の構造　資料(3)の図15を引用して略記

(4) Huang, B., Zhang, K., Zhang, J., Ramsey, J. D., Sanchez-Romero, R., Glymour, C., & Schölkopf, B. (2020). Causal Discovery from Heterogeneous/Nonstationary Data. J. Mach. Learn. Res., 21(89), 1-53.

　以下にCPIデータを使ったテストコードを示します。

from causallearn.search.ConstraintBased.CDNOD import cdnod

# default parameters
c_indx = np.reshape(np.asarray(list(range(data.shape[0]))), (data.shape[0],1))
cg = cdnod(data, c_indx)

# or customized parameters
#cg = cdnod(data, c_indx, alpha, indep_test, stable, uc_rule, uc_priority, mvcdnod, correction_name, background_knowledge, verbose, show_progress)

# visualization using pydot
# note that the last node is the c_indx
cg.draw_pydot_graph(labels=['usdjpy', 'cpi','con'])

# or save the graph
from causallearn.utils.GraphUtils import GraphUtils

pyd = GraphUtils.to_pydot(cg.G)
pyd.write_png('test3.png')

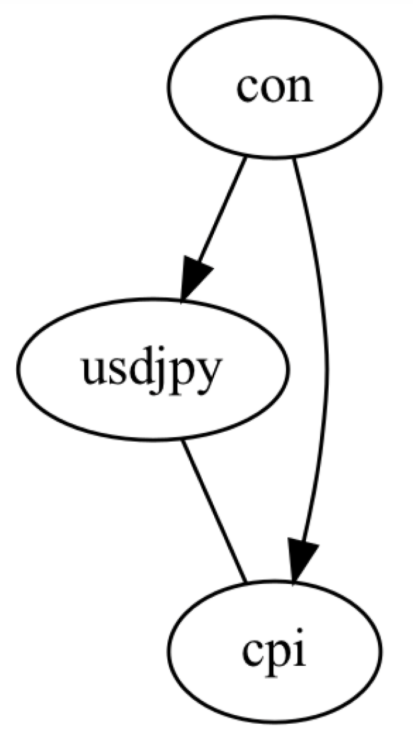
図5　観測されない交絡因子を含むDAG

図５の出力グラフは、conで示す交絡因子がusdjpyとcpiに影響していることを示します。

Granger因果性

　前述のベクター自己回帰モデル(VAR)を用いたものです。causal-learnに実装されたGrangerのAPIを用いてCPIデータに適用します。戻り値には、P-値の行列と、係数が出力されます。

from causallearn.search.Granger.Granger import Granger
G = Granger()
p_value_matrix = G.granger_test_2d(data)
coeff = G.granger_lasso(data)
print(p_value_matrix)
coeff

(array([[0.    , 0.0234, 0.    , 0.0088],
       [0.0543, 0.    , 0.03  , 0.    ]]), array([[1, 0, 1, 1],
       [0, 1, 0, 1]]))
array([[ 0.98162114,  0.14997314, -0.01041117,  0.        ],
       [ 0.00860737,  0.99358639, -0.00414914,  0.        ]])

線形非ガウシアン非周期モデル　（LiNGAM)

　上記とは別のアプローチとして、これ以後、抑制関数因果モデルを用いたアルゴリズムのAPIでデータを扱います。

　このモデルは、因果モデルのノイズ項が非ガウシアンであることを仮定します。

　causal-learnは公式な線形非ガウシアン非周期モデル（Linear Non-Gaussian Acyclic Model :LiNGAM）　の実装には、以下のアルゴリズムが含まれます。

ICA-based LiNGAM
Direct LiNGAM
VAR-LiNGAM
RCD
CAM-UV

　DAGで記述したLiNGAMのモデルの例を図５に示します。観測値x_i, i {1,..m}は因果の順序で並べられ、生成過程は帰納的です。

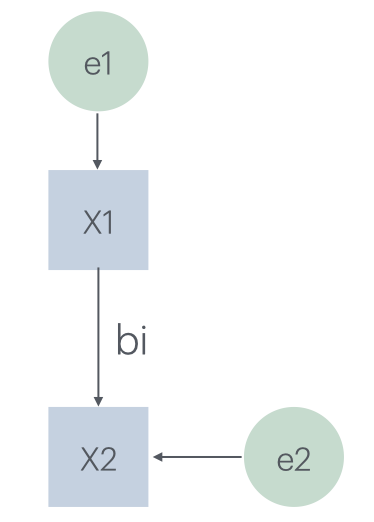
図6　LiNGAMモデルのDAG例

　各変数x_iは、先に割り当てられた変数の線形関数として割り当てられます。これにノイズ項e_iと定数c_iが追加され、以下のように定義されます。

x_i = Σ b_ij x_j + e_i + c_i

　ノイズ項のe_iは、非ガウシアン分布の一定のランダム変数です。e_iは互いに独立しています。

　各変数をベクターで表すと、

  x = Bx + e
  x = Ae       ----------(*)
  A =(I-B)^-1

　ICAは上の（*）で与えられるような線形モデルを識別するための、最近の統計的な技術です。モデルの詳細は以下の論文⁽⁵⁾に解説されています。

(5) Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A., & Jordan, M. (2006). A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(10).

以下はこのICA-based LiNGAMのAPIを使ったコードです。パラメータはデフォルト設定を用いています。

from causallearn.search.FCMBased import lingam
#model = lingam.ICALiNGAM(random_state, max_iter)
#model.fit(X)
# Default
model = lingam.ICALiNGAM()
model.fit(df)
print(model.causal_order_)
print(model.adjacency_matrix_)

[0, 1]
[[0.         0.        ]
 [0.13743561 0.        ]]

Direct LiNGAM

from causallearn.search.FCMBased import lingam
#model = lingam.DirectLiNGAM(random_state, prior_knowledge, apply_prior_knowledge_softly, measure)
#model.fit(X)
# Default
model = lingam.DirectLiNGAM()
model.fit(df)

print(model.causal_order_)
print(model.adjacency_matrix_)

[1, 0]
[[0.         3.83289287]
 [0.         0.        ]]

VAR-LiNGAM

from causallearn.search.FCMBased import lingam
#model = lingam.VARLiNGAM(lags, criterion, prune, ar_coefs, lingam_model, random_state)
#model.fit(X)
model = lingam.VARLiNGAM()
model.fit(df)

print(model.causal_order_)
print(model.adjacency_matrices_[0])
print(model.adjacency_matrices_[1])
#print(model.residuals_)

[1, 0]
[[0. 0.]
 [0. 0.]]
[[9.93327482e-01 6.84479106e-02]
 [7.98436862e-05 1.01790137e+00]]

事後非線形因果モデル　（PNL因果モデル）

　Post nonlinear(PNL) causal models.

　PNL因果モデルでは、因果の構造はDAGによって示され、各変数x_iは次式で示されます。

x_i = f_i,2(f_i,1(pa_i) +e_i), i=1,...,n,

　これは特別なケースとして、加法的ノイズモデルを含みます。そのモデルは上記の式でx_iの非線形ディストーションf_i,2が存在しないケースに相当します。

　PNL因果モデルの詳細は以下の論文⁽⁶⁾で解説されています。

(6) Zhang, K., & Hyvärinen, A. (2009, June). On the Identifiability of the Post-Nonlinear Causal Model. In 25th Conference on Uncertainty in Artificial Intelligence (UAI 2009) (pp. 647-655). AUAI Press.

from causallearn.search.FCMBased.PNL.PNL import PNL
pnl = PNL()
p_value_foward, p_value_backward = pnl.cause_or_effect(data_x, data_y)
print(p_value_foward)
print(p_value_backward)

[0.]
[0.116]

加法的ノイズモデル

Additive noise models

Hoyer, P. O., Janzing, D., Mooij, J. M., Peters, J., & Schölkopf, B. (2008, December). Nonlinear causal discovery with additive noise models. In NIPS (Vol. 21, pp. 689-696).

from causallearn.search.FCMBased.ANM.ANM import ANM
anm = ANM()

p_value_foward, p_value_backward = anm.cause_or_effect(data_x, data_y)
print(p_value_foward)
print(p_value_backward)

0.0
0.0

参考資料

(1) Spirtes, P., Glymour, C. N., Scheines, R., & Heckerman, D. (2000). Causation, prediction, and search. MIT press.
(2) Spirtes, P., Meek, C., & Richardson, T. (1995, August). Causal inference in the presence of latent variables and selection bias. In Proceedings of the Eleventh conference on Uncertainty in artificial intelligence (pp. 499-506).
(3) S. Lauritzen.(1996). Graphical Models. Oxford University Press.
(4) Huang, B., Zhang, K., Zhang, J., Ramsey, J. D., Sanchez-Romero, R., Glymour, C., & Schölkopf, B. (2020). Causal Discovery from Heterogeneous/Nonstationary Data. J. Mach. Learn. Res., 21(89), 1-53.
(5) Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A., & Jordan, M. (2006). A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(10).
(6) Zhang, K., & Hyvärinen, A. (2009, June). On the Identifiability of the Post-Nonlinear Causal Model. In 25th Conference on Uncertainty in Artificial Intelligence (UAI 2009) (pp. 647-655). AUAI Press.
Hoyer, P. O., Janzing, D., Mooij, J. M., Peters, J., & Schölkopf, B. (2008, December). Nonlinear causal discovery with additive noise models. In NIPS (Vol. 21, pp. 689-696).
"Causality Models,Reasoning, and Inference" Judea Pearl

causal-learnによる因果探索

causal-learnの因果探索アルゴリズム

causal-learnのインストール

データの準備

Peter-Clark(PC)アルゴリズム

高速因果推論(Fast Causal Inference)

CD-NOD

Granger因果性

線形非ガウシアン非周期モデル　（LiNGAM)

Direct LiNGAM

VAR-LiNGAM

事後非線形因果モデル　（PNL因果モデル）

加法的ノイズモデル

参考資料

グラフィカル・モデルを基にした因果探索

JupyterノートブックでRを使う方法

ドル円為替レートと物価上昇の関係：非線形モデル

Apple Silicon Mac の　R バージョン更新・インストール

書評：Essential Math for AI

causal-learnによる因果探索

causal-learnの因果探索アルゴリズム

causal-learnのインストール

データの準備

Peter-Clark(PC)アルゴリズム

高速因果推論(Fast Causal Inference)

CD-NOD

Granger因果性

線形非ガウシアン非周期モデル （LiNGAM)

Direct LiNGAM

VAR-LiNGAM

事後非線形因果モデル （PNL因果モデル）

加法的ノイズモデル

参考資料

線形非ガウシアン非周期モデル　（LiNGAM)

事後非線形因果モデル　（PNL因果モデル）