クレジット・カードの種別と利用額の最適化　YLearnによる因果推論(2)

YLearn因果推論パッケージを使ったケース・スタディを使ってYLearnの機能を解説します。YLearnの因果推論パイプラインを使ったマーケティング上の分析の一つになります。クレジット・カードのグレードを更新した場合の効果の推論です。

機能と仕様

　以下、簡単に機能をまとめ、最後にケーススタディを使って動作を確認します。ケース・スタディでは、Kaggleの実際のデータセットを使います。

DAG グラフと交絡因子

　観測されていない変数はconfounding arcとして定義し、下の図１では(黒の点線)で示すように両端に矢印のある曲線で表示しています。

from ylearn.causal_model.graph import CausalGraph
causation = {
        'X': ['Z2'],
    'Z1': ['X', 'Z2'],
    'Y': ['Z1', 'Z3'],
    'Z3': ['Z2'],
    'Z2': [],
}
arcs = [('X', 'Z2'), ('X', 'Z3'), ('X', 'Y'), ('Z2', 'Y')]

cg = CausalGraph(causation=causation, latent_confounding_arcs=arcs)

list(cg.c_components)

[{'X', 'Y', 'Z2', 'Z3'}, {'Z1'}]

　因果の構造の中でバックドアを調べます。

from ylearn.causal_model.graph import CausalGraph
from ylearn.causal_model.model import CausalModel

causation = {
    'X1': [],
    'X2': [],
    'X3': ['X1'],
    'X4': ['X1', 'X2'],
    'X5': ['X2'],
    'X6': ['X'],
    'X': ['X3', 'X4'],
    'Y': ['X6', 'X4', 'X5', 'X'],
}

cg = CausalGraph(causation=causation)
cm = CausalModel(causal_graph=cg)
backdoor_set, prob = cm.identify(treatment={'X'}, outcome={'Y'}, identify_method=('backdoor', 'simple'))['backdoor']

print(backdoor_set)

['X3', 'X4']

CausalModel

　このオブジェクトは、因果関係を識別を実行しIV(Instrumental variable)を探します。

　Pearlの因果の梯子におけるinterventionを定義し実行します。Pearlの推論の梯子とintervention, counterfactualについて、本サイトの別の因果推論に関するブログでも解説しています。

　CausalModelがサポートしている識別法をモデルに定義します。注意：全ての因果の影響が統計的な推定に変換できるわけではありません。

　CausalModelによって提供されている因果の影響の識別を以下にリストします。

• Backdoor adjustment

doオペレータによって、Xのyに対する影響は、以下のように定義されます。
　P(y|do(x)) = Σ P(y|x,w) P(w)
変数Wのセットが満足されるなら、backdoor 基準になります。

• Frontdoor adjustment

XからYへの因果の影響は、以下のように定義されます。
　P(y~ do (x)) =ΣP(w|x) ΣP(y|x',w)P(x')
　変数Wがfront-door 基準を満足します。

• General Identification

Instrumental variableを発見することです。
XとYの間に観測されていない交絡因子があれば、Instrumental variableは、Yに対するXの影響を推定することと識別することに役立ちます。
Zの変数のセットはinstrumental variableと呼ばれます。

1. zはXの因果の影響を持ちます。
2. Yへのzの因果の影響は、Xの中間に経由します。
3. zからYへのbackdoor経路はありません。

　因果の構造で、全ての観測されていない変数は削除され、関連する因果はconfounding arc(両端に矢印のある黒の点線：図１参照)によってに取り替えられます。

(1) general identification法を使ってXのYに対する因果の影響を識別します。

from ylearn.causal.model.graph import CausalGraph
causation = {
	'X': ['Z'],
	'Z1':['X', 'Z2'],
	'Y':['Z1', 'Z3'],
	'Z3':['Z2'],
	'Z2'][]
}
arcs = [{'X','Z2'},{'Z','Z3'},{'X','Y'},{'Z2','Y'}]
cg = CausalGraph(causation=causation, latent_confounding_arcs = arcs)

from ylearn.causal_model.model import CausalModel
cm = CausalModel(causal_model=cg)
stat_estimand = cm.id(y={'y', x={'x'})
stat_estimand.shoe_latex_expression()

　関数はDAG自体を表示しないので、DAGのイメージを別途、記述しておいた方が良いでしょう。DAGを見れば出力結果が分かりやすいと思います。

　DAGは以下の図１のイメージで因果関係を示しています。p,t,l,gによる因果の構造です。

図１　p,t,l,gにより因果の構造

Instrumental Variable(IV)を取得します。この因果の構造では、t,gに対するIVとしてPが出力されます。

causation = {
    'p':[],
    't': ['p', 'l'],
    'l': [],
    'g': ['t', 'l']
}
arc = [('t', 'g')]
cg = CausalGraph(causation=causation, latent_confounding_arcs=arc)
cm = CausalModel(causal_graph=cg)

cm.get_iv('t', 'g')

{'p'}

確率の表示

from ylearn.causal_model.prob import Prob

var = {'v'}
conditional = {'y'} # the conditional set
marginal = {'w'} # sum on w

p1 = Prob(variables={'w'}, conditional={'z'})
p2 = Prob(variables={'x'}, conditional={'y'})
p3 = Prob(variables={'u'})
product = {p1, p2, p3}

P = Prob(variables=var, conditional=conditional, marginal=marginal, product=product)
P.show_latex_expression()

図２　上のコード出力

P.parse()

'\\sum_{w}P(v|y)\\left[P(x|y)\\right]\\left[P(w|z)\\right]\\left[P(u)\\right]'

Estmatorの使い方

　以下の手続きで任意のEstimatorModelを適用することができます。

1. pandas データフレームの中に、treatment,outcome,adjustment,covariateの名称でデータをセットします。
2. EstimatorModelオブジェクトのfit()メソッドにデータを渡してコールします。
3. テストデータに適合したEstimatorModelオブジェクトを使いestmate()メソッドをコールします。

　YLearnのこの手続きを使ったケース・スタディがあります。以下がサンプルコードです。(Double Machine Learningの例)

　これは統計的な手法では解決できない、パラメトリックな関数でモデル化できない場合に、機械学習の方法を使って推定する方法です。

【DoubleML】

from sklearn.ensemble import RandomForestRegressor

from ylearn.exp_dataset.exp_data import single_continuous_treatment
from ylearn.estimator_model.double_ml import DoubleML

# build the dataset
train, val, treatment_effect = single_continuous_treatment()
adjustment = train.columns[:-4]
covariate = 'c_0'
outcome = 'outcome'
treatment = 'treatment'

dml = DoubleML(x_model=RandomForestRegressor(), y_model=RandomForestRegressor(), cf_fold=3,)
dml.fit(train, outcome, treatment, adjustment, covariate,)

DoubleML(x_model=RandomForestRegressor(random_state=2022), y_model=RandomForestRegressor(random_state=2022), yx_model=LinearRegression(), cf_fold=3)

【Doubly Robust】

import numpy as np
from numpy.random import multivariate_normal

from sklearn.ensemble import RandomForestClassifier, GradientBoostingRegressor

import matplotlib.pyplot as plt

from ylearn.estimator_model.meta_learner import SLearner, TLearner, XLearner
from ylearn.estimator_model.doubly_robust import DoublyRobust
from ylearn.exp_dataset.exp_data import binary_data
from ylearn.utils import to_df

# build the dataset
d = 5
n = 2500
n_test = 250

y, x, w = binary_data(n=n, d=d, n_test=n_test)
data = to_df(outcome=y, treatment=x, w=w)
outcome = 'outcome'
treatment = 'treatment'
adjustment = data.columns[2:]

# build the test dataset
treatment_effect = lambda x: (1 if x[1] > 0.1 else 0) * 8

w_test = multivariate_normal(np.zeros(d), np.diag(np.ones(d)), n_test)
delta = 6/n_test
w_test[:, 1] = np.arange(-3, 3, delta)

dr = DoublyRobust(
    x_model=RandomForestClassifier(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
    y_model=GradientBoostingRegressor(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
    yx_model=GradientBoostingRegressor(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
    cf_fold=1,
    random_state=2022,
)
dr.fit(data=data, outcome=outcome, treatment=treatment, covariate=adjustment,)
dr_pred = dr.estimate(data=data, quantity=None).squeeze()

dr_pred

array([ 0.39991563,  8.34665887, -0.27504074, ..., -0.41869917,
        5.21264942, 11.84913746])

　Random Forestなどは、sklearnの拡張モジュールがx86向けのオブジェクトファイルになっており、arm64をサポートしていません。import時に互換性の問題でエラーになります。

　sklearn_ex/配下の参照ファイルは、推論メソッドやpolicy interpreterなどもx86用のオブジェクトがバンドルされており、ImportErrorになります。

　Apple Silicon Macでは多くの機能は使えません。

　以下、YLearnを使ったケーススタディを示します。これを使って、Apple Silicon Mac上で動作するAPIの機能とylearnの因果推論を見てみていきます。

ケース・スタディ：銀行顧客の取引額

　ここでは、典型的な銀行の顧客のデータセットを使って、YLearnの Why APIの使い方を解説します。Whyは、因果探索、因果の影響の識別、因果の影響の推定、counterfactual推論、ポリシーの学習（最適化）を含む、因果学習パイプラインの全ての処理を取り扱います。

　最初にWhyインスタンスを作成し、fit()メソッドを呼び出して訓練する必要があります。plot_causal_graph(),causal_effect(),whatif()のようなユーティリティは、いくつかのcounterfactualシナリオを分析するために実行します。その他の鍵になるメソッドpolicy_interpreter()は、出力を最適化するためにカスタマイズしたソリューションを提供します。

データセット

　以下は、KaggleのWebサイトです。Kaggleは、機械学習のコミュニティ・サイトで様々なデータセットを利用することができます。

https://www.kaggle.com/datasets/syviaw/bankchurners

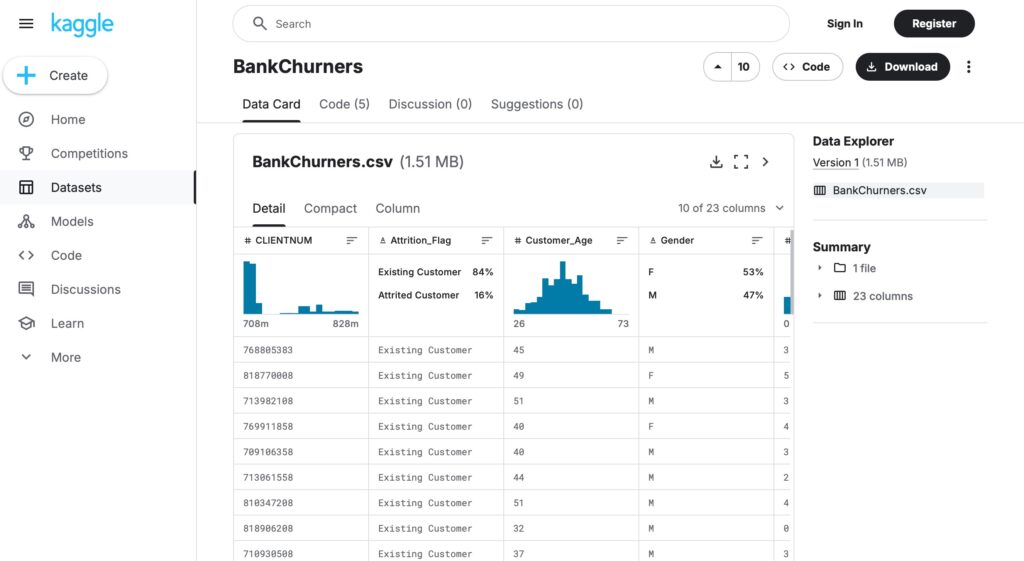
　KaggleのBankChurnersデータセットのサブセットを使います。そのデータセットを取引総額の原因を分析するために使い、取引額を最大化するための特別なストラテジーを提供します。データセットは、１００００人の顧客の情報を含むデータセットで、ユーザーの特徴を説明する２０分類変数からなります。ここでは因果関係と因果の影響を分析するために１０変数を選択します。

• 顧客の一般的な特徴：年齢など
• 顧客の信販カードの特徴：カード分類、利用限度額など
• 顧客の取引額：総取引額

　変数Total_Trans_Amtで示す総取引額が、結果になります。

　最初に、必要なライブラリをインポートします。

import numpy as np
import pandas as pd
from matplotlib import pyplot  as plt

from sklearn.model_selection import train_test_split
from ylearn import Why
import warnings
warnings.filterwarnings('ignore')

　次にデータセットを読み込みます。データセットは、BankChurners.csv.zipという名称で、csvファイルで提供されています。ローカルフォルダにダウンロードしておきます。

df = pd.read_csv('ylearn/BankChurners.csv.zip')
cols = ['Customer_Age', 'Gender', 'Dependent_count', 'Education_Level', 'Marital_Status', 'Income_Category', 
        'Months_on_book', 'Card_Category', 'Credit_Limit',  
        'Total_Trans_Amt' 
     ]
data = df[cols]
outcome = 'Total_Trans_Amt'

data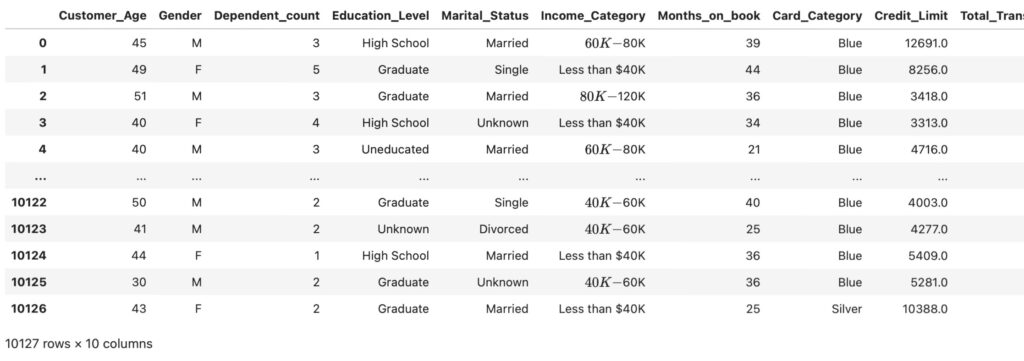 

　クロス・バリデーションを実行するため、データを訓練用とテスト用に分離します。

train_data,test_data=train_test_split(data,test_size=0.3,random_state=123)

print('train_data:',train_data.shape)
print('test_data: ',test_data.shape)

train_data: (7088, 10)
test_data:  (3039, 10)

カード分類の統計

　上のデータセットで示す、三つのクレジット・カードの特徴、カードの種別(Card_Category)は、分類の一つであり、処置の対象としては妥当な変数です。カード分類の概要と対応する利用額の平均値を以下に示します。

card_stat=train_data[['Card_Category','Total_Trans_Amt']].groupby('Card_Category').agg(['mean','min','max',]).sort_values(by=('Total_Trans_Amt','mean'))

card_stat[('Total_Trans_Amt','mean')].plot(kind='bar', title='Mean of Total_Trans_Amt')
card_stat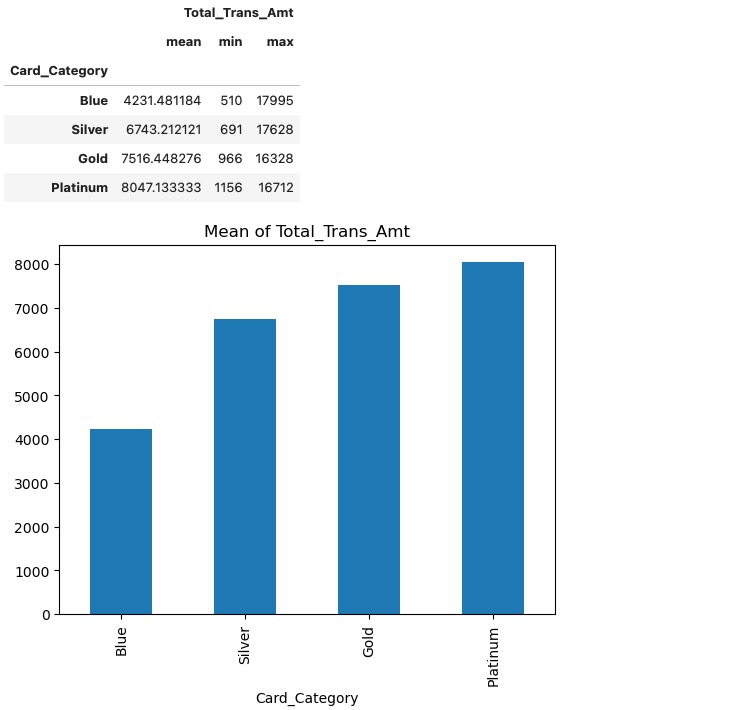

　最初にWhyインスタンスを生成します。その後、treatment='Card_Category' と定義し、fit()メソッドを使ってモデルを訓練します。

why=Why()
why.fit(train_data,outcome,treatment='Card_Category')

Why(discrete_outcome=False, discrete_treatment=True)

因果の影響の推定

　カードは４つの種別の分類、Blue,Silver,Gold,Platinumがあります。Blueを観測基準の変数として、残りの３種類を処置変数とし、causal_effectメソッドが３種の因果の影響を推定します。結果から、カードのアップグレードが個人の利用額を増加させることがわかります。ゴールドカード(Gold)が最も高い効果を持っています。

effect=why.causal_effect(control='Blue',return_detail=True)
effect=effect.loc['Card_Category'].sort_values(by='mean')
details=effect.pop('detail')

plt.figure(figsize=(10, 5))
plt.violinplot(details.tolist(), showmeans=True)
plt.ylabel('Effect distribution')
plt.xticks(range(1,len(effect)+1), details.index.tolist())
plt.plot( [0, ]*(len(effect)+2) )
plt.show()

effect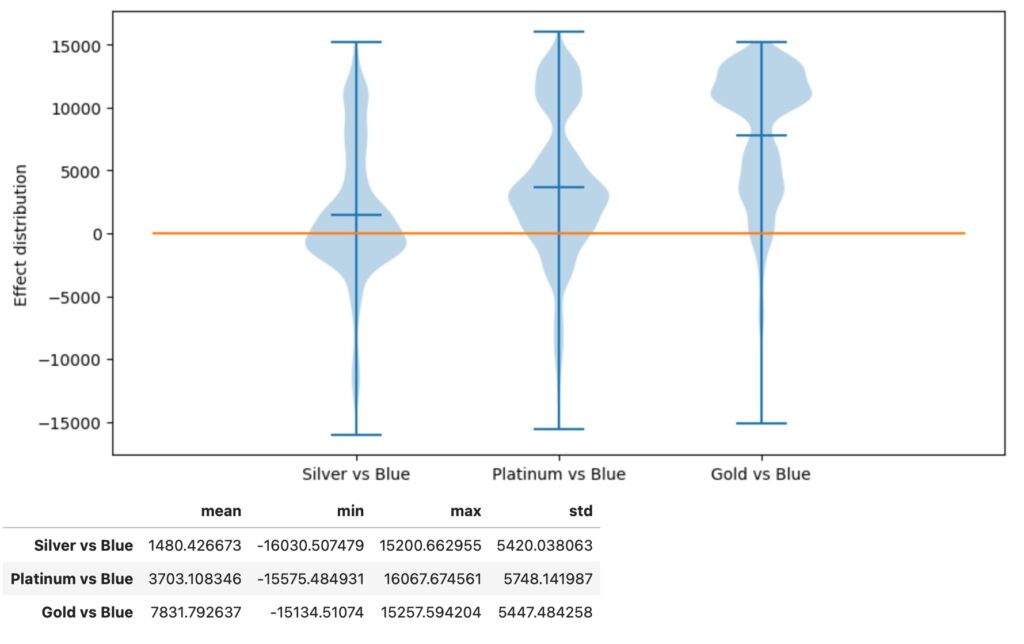

Counterfactual推論

　意思決定の責任者は、顧客のカードの種別を更新した場合の推定増加分を知りたいものです。whatif() APIは、そのcounterfactual推論（もしそうであれば、どうなるか）を実行するためのソリューションを提供します。

• すべてのBlueカードをSilverに更新した場合

whatif_data= train_data[lambda df: df['Card_Category']=='Blue' ]
out_orig=whatif_data[outcome]

value_sliver=whatif_data['Card_Category'].map(lambda _:'Silver')
out_silver=why.whatif(whatif_data,value_sliver,treatment='Card_Category')

print('Selected customers:', len(whatif_data))
print(f'Mean {outcome} with Blue card:\t{out_orig.mean():.3f}' )
print(f'Mean {outcome} if Silver card:\t{out_silver.mean():.3f}' )

plt.figure(figsize=(8, 5), )
out_orig.hist(label='Blue card',bins=30,alpha=0.7)
out_silver.hist(label='Silver card',bins=30,alpha=0.7)
plt.legend()

Selected customers: 6590
Mean Total_Trans_Amt with Blue card:	4231.481
Mean Total_Trans_Amt if Silver card:	5749.053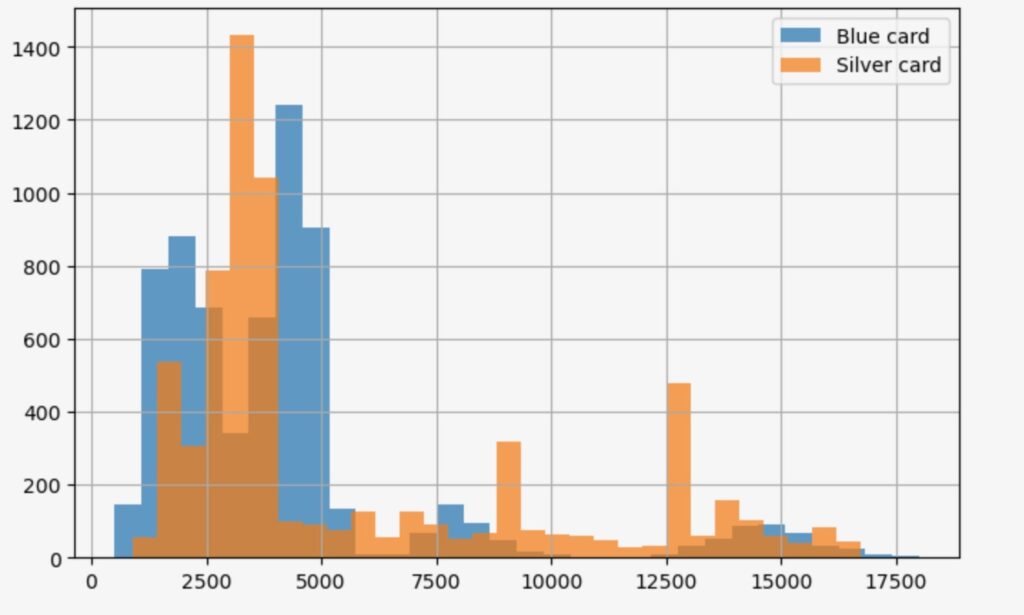

• すべてのBlueカードをGoldに更新した場合

whatif_data= train_data[lambda df: df['Card_Category']=='Blue' ]
out_orig=whatif_data[outcome]

value_gold=whatif_data['Card_Category'].map(lambda _:'Gold')
out_gold=why.whatif(whatif_data,value_gold,treatment='Card_Category')


print('Selected customers:', len(whatif_data))
print(f'Mean {outcome} with Blue card:\t{out_orig.mean():.3f}' )
print(f'Mean {outcome} if Gold card:\t{out_gold.mean():.3f}' )

plt.figure(figsize=(8, 5), )
out_orig.hist(label='Blue card',bins=30,alpha=0.7)
out_gold.hist(label='Gold card',bins=30,alpha=0.7)
plt.legend()

Selected customers: 6590
Mean Total_Trans_Amt with Blue card:	4231.481
Mean Total_Trans_Amt if Gold card:	12430.841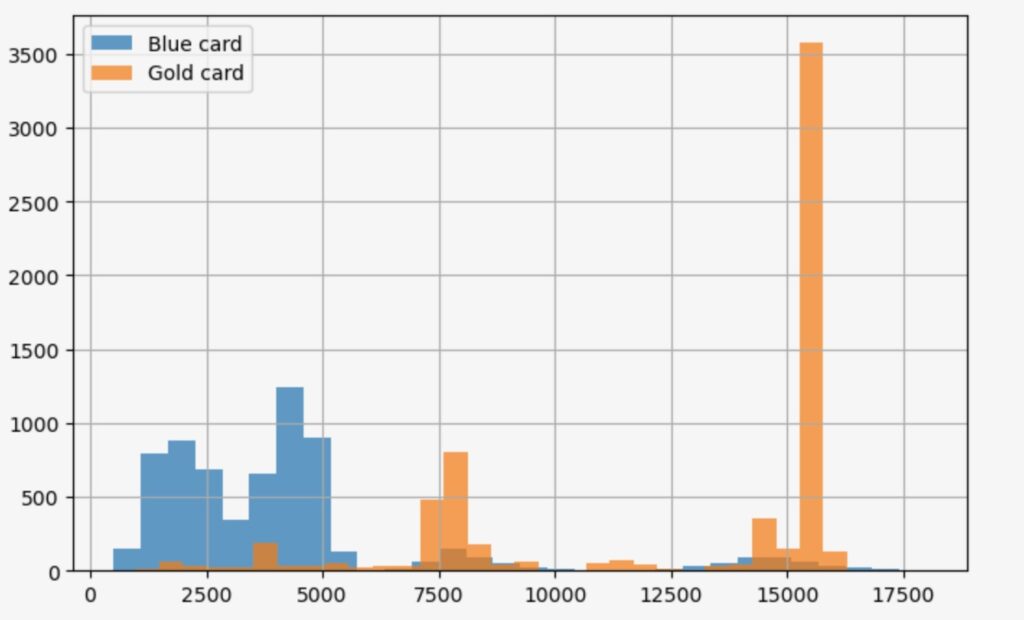

• すべてのBlueカードをPlatinumに更新した場合

whatif_data= train_data[lambda df: df['Card_Category']=='Blue' ]
out_orig=whatif_data[outcome]

value_platinum=whatif_data['Card_Category'].map(lambda _:'Platinum')
out_platinum=why.whatif(whatif_data,value_platinum,treatment='Card_Category')


print('Selected customers:', len(whatif_data))
print(f'Mean {outcome} with Blue card:\t{out_orig.mean():.3f}' )
print(f'Mean {outcome} if Platinum card:\t{out_platinum.mean():.3f}' )

plt.figure(figsize=(8, 5), )
out_orig.hist(label='Blue card',bins=30,alpha=0.7)
out_platinum.hist(label='Platinum card',bins=30,alpha=0.7)
plt.legend()

Selected customers: 6590
Mean Total_Trans_Amt with Blue card:	4231.481
Mean Total_Trans_Amt if Platinum card:	8047.359

　BlueカードをSilver, Gold, Platinumカードに更新することによって、Total_Trans_Amt 利用総額は、それぞれ、4231から5651、12477、8044に増加します。これは、期待の持てる改善です。しかし、すべてのBlueカードをGoldに更新することを最適化したソリューションとして良いでしょうか。

　ここでYLearnは、最適化したソリューションを探すために、policy_interpreter()メソッドを提供しています。しかしosx版はx86用のオブジェクトが提供されており、AppleSiliconでは動作しません。そのため、最適化のAPIの動作確認はできませんでした。

　YLearnでは因果探索メソッドを使って、因果関係を探すことができます。そのためにデフォルトの設定でfit()メソッドを使います。手続きは省略しますが、その結果gender(性別)とEducation_level(教育水準)が重要な因子として識別されたこととします。(Apple Siliconで動作しないため）

訓練データでの因果の影響の推定

メソッドの使い方を示します。'M'(性別)と'College'(教育水準）を処置とすることによって、因果の影響を推定します。

why.causal_effect(control=['M','College'])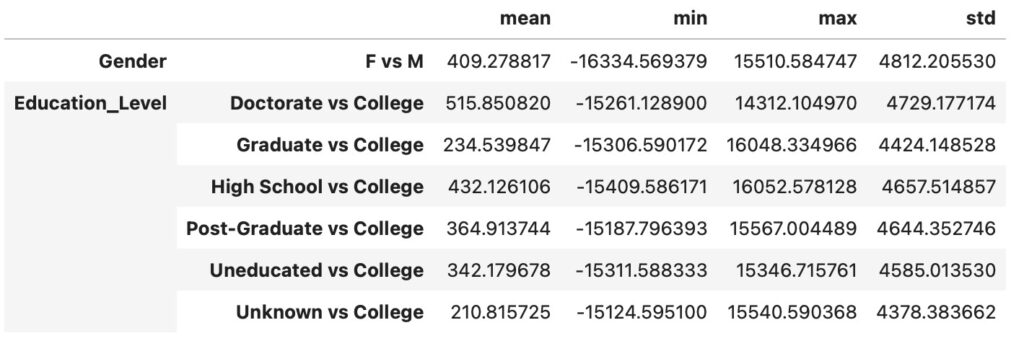

テストデータでの因果の影響の推定

　テストデータの因果の影響の推定を示します。

why.causal_effect(test_data, control=['M','College'])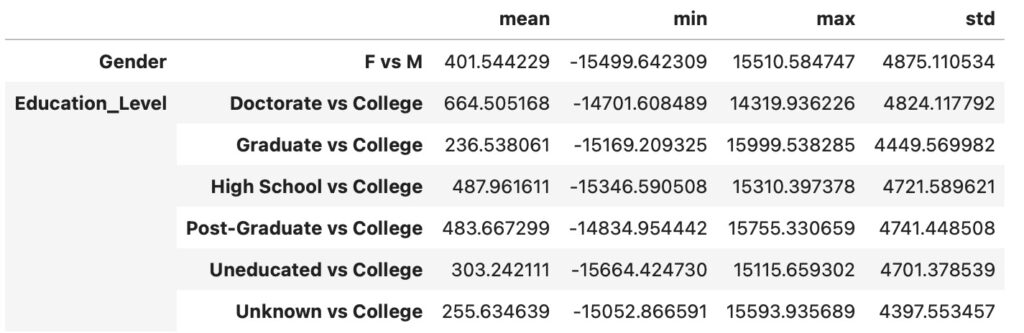

　性別と教育水準は、特徴に属してますが、処置の対象としては現実的ではありません。訓練データとテストデータの推定結果は、とても類似しており、メソッドの頑丈さを示しています。

参考資料