【マネーサプライと物価上昇の因果推論】で、線形モデルを適用して因果関係を調べてみました。物価上昇がドル円為替レートと因果関係があり、国内の金融政策には影響を受けていないことを示しました。ここでは、このドル円為替レートと物価上昇の関係に非線形なモデルを適用した例を示します。
USDJPY為替レートと物価上昇
最初に、【マネーサプライと物価上昇の因果推論】で使った同じデータセットを読み込みます。
図1 CPIーUSDJPY為替レートのデータセット
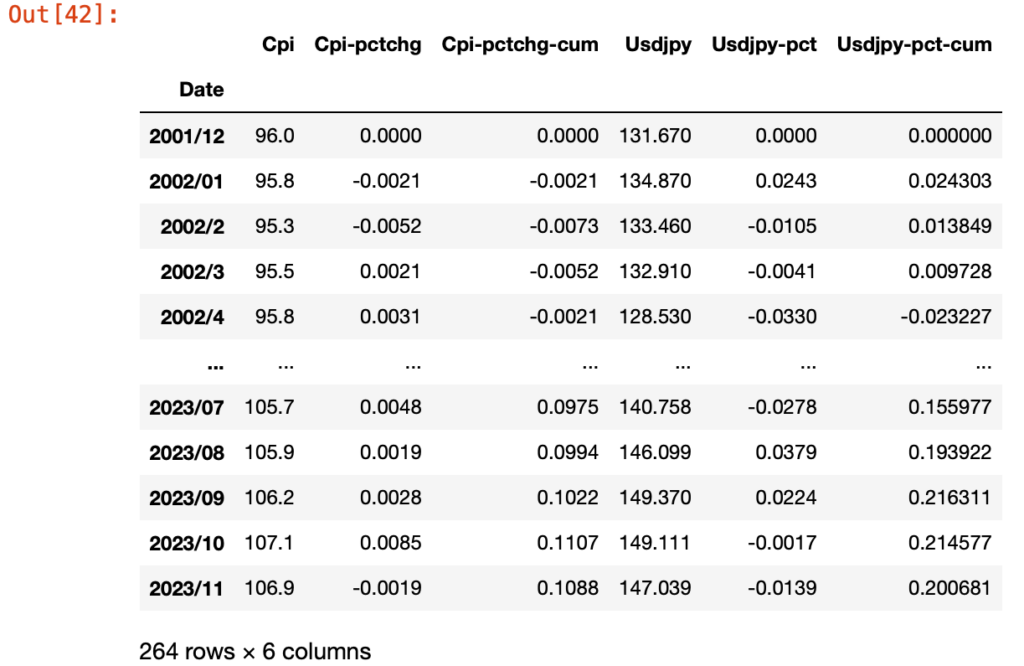
このデータセット(期間2001年12月〜2023年11月のCPIとUSD JPY為替レート)を用いて、以下のように線形な関係があることを仮定してモデル化しました。
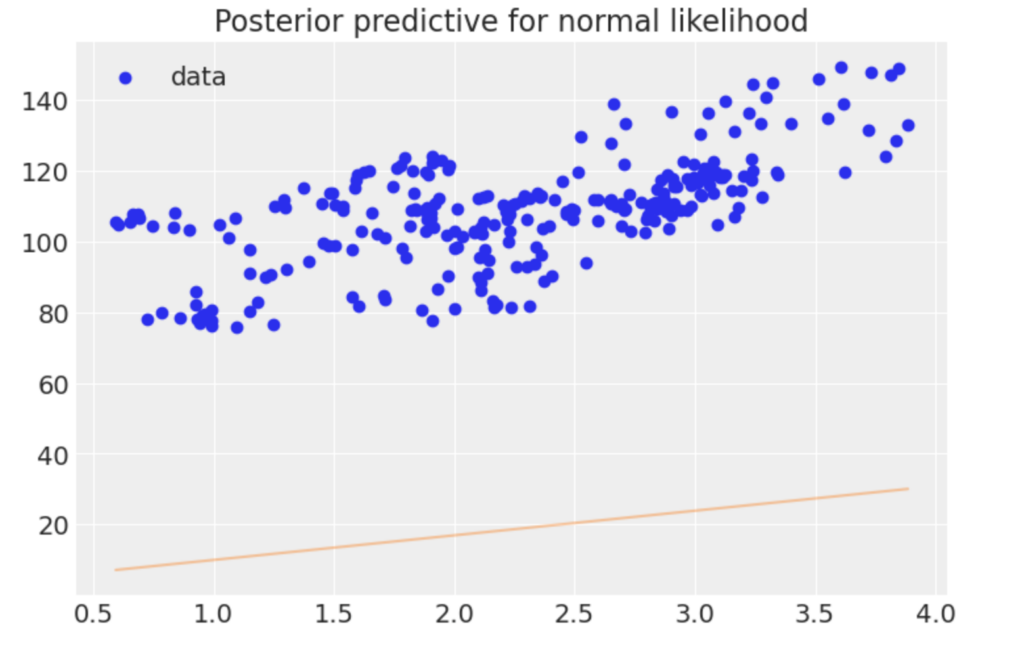
図2 USDJPY為替レート-CPI線形回帰
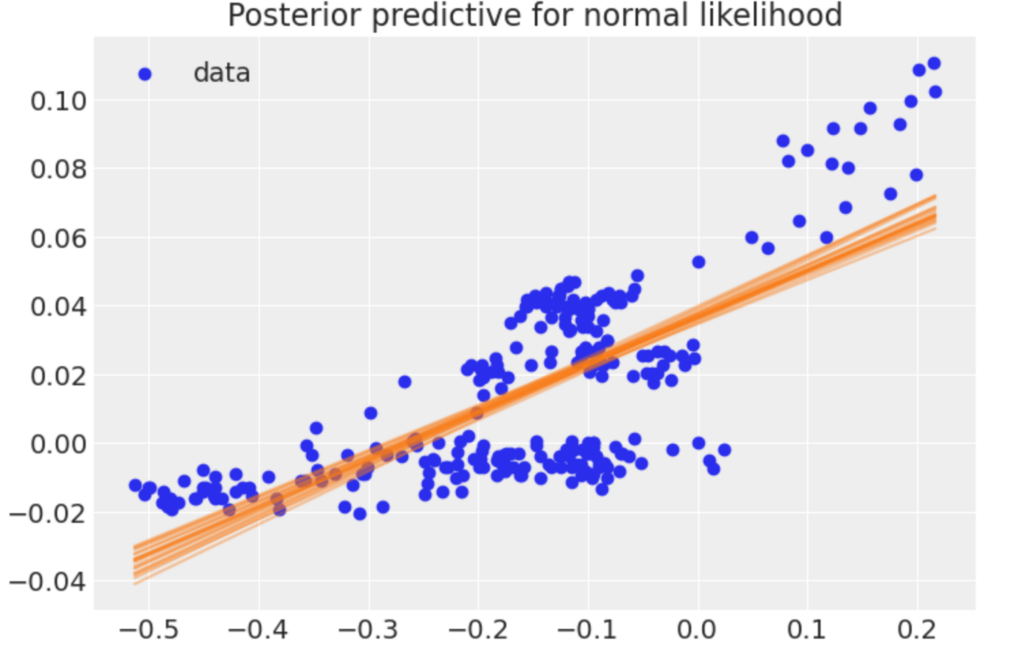
ここでCPIとUSDJPY為替レートの関係を見るとCPIがマイナス領域にある場合に、一塊のデータセットがあるように見えます。これは2000年〜2004年, 2006-2012年にかけて、継続的に物価が下落している部分のデータです。CPIがプラスの領域とはスロープの値が異なるデータセットがあります。これを以下のように二つのデータ領域に分割して分析します。
図3 二つの部分からなるデータセット
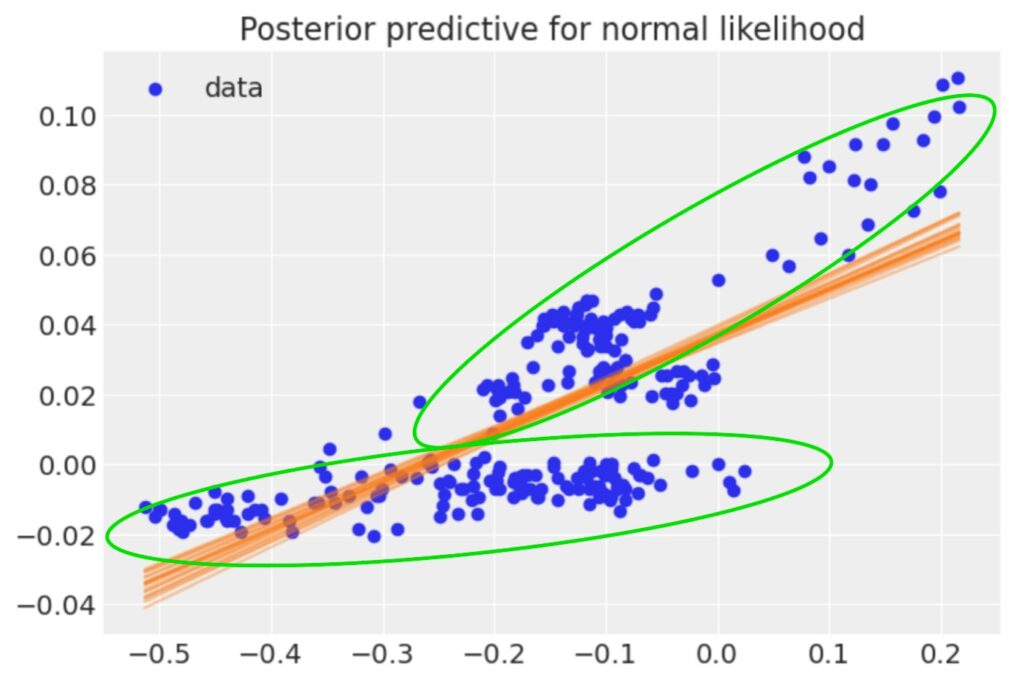
以下の図に示すように、円の対ドル為替レートが下落する局面では、 CPIは下落し、為替が上昇する局面では、CPIも上昇しています。
図4 CPIとUSD JPY為替レートの推移(2001年12月〜2023年11月)
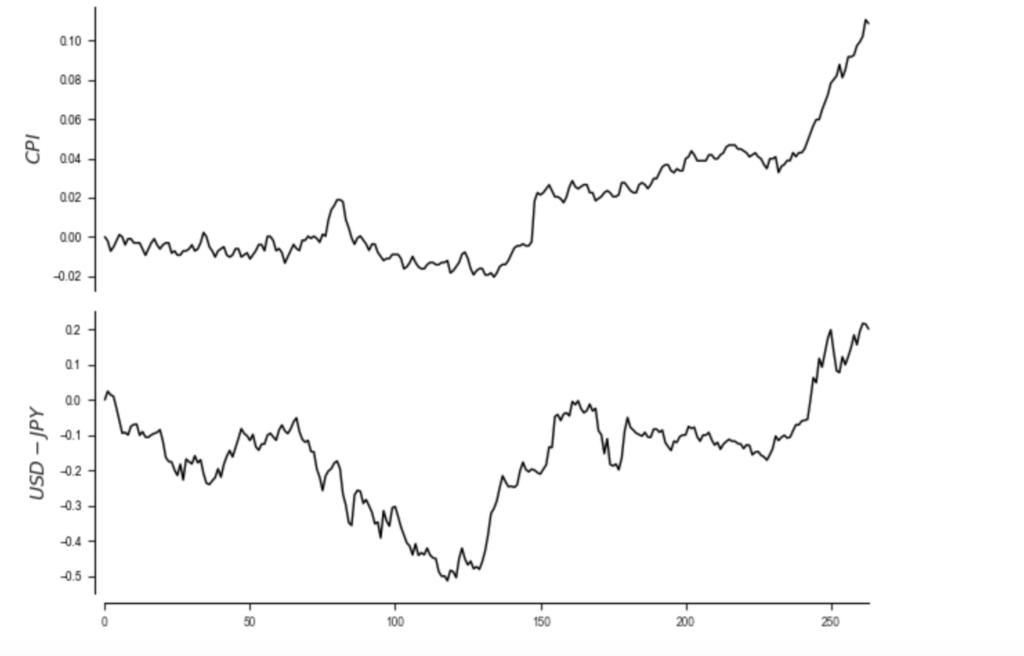
CPIが0近辺かそれ以下で推移する場合は、物価の下落に価格硬直製があって、下落率が低い傾向があります。価格設定において、値上げより、値下げの方が反応が緩やかな傾向です。これには市場取引による需給に基づく価格形成だけでなく、営利活動におけるプライシングする側の心理的な要因が関係していると考えられます。
また、USDJPY為替レートに着目すると日本で長期の低金利政策が取られているため、FEDの金融政策に依存する度合いが強いことがわかります。
日米金利差とUSDJPY為替レート
以下の図5に日米金利差を示します。長期金利として日米10年債の金利差とUSDJPY為替レートの関係を示しています。
ドル円為替レートのトレンドは、長期金利差の影響を受けて推移しています。
図5 JGBとT-Bond(10年債)の金利差とUSDJPY為替レート
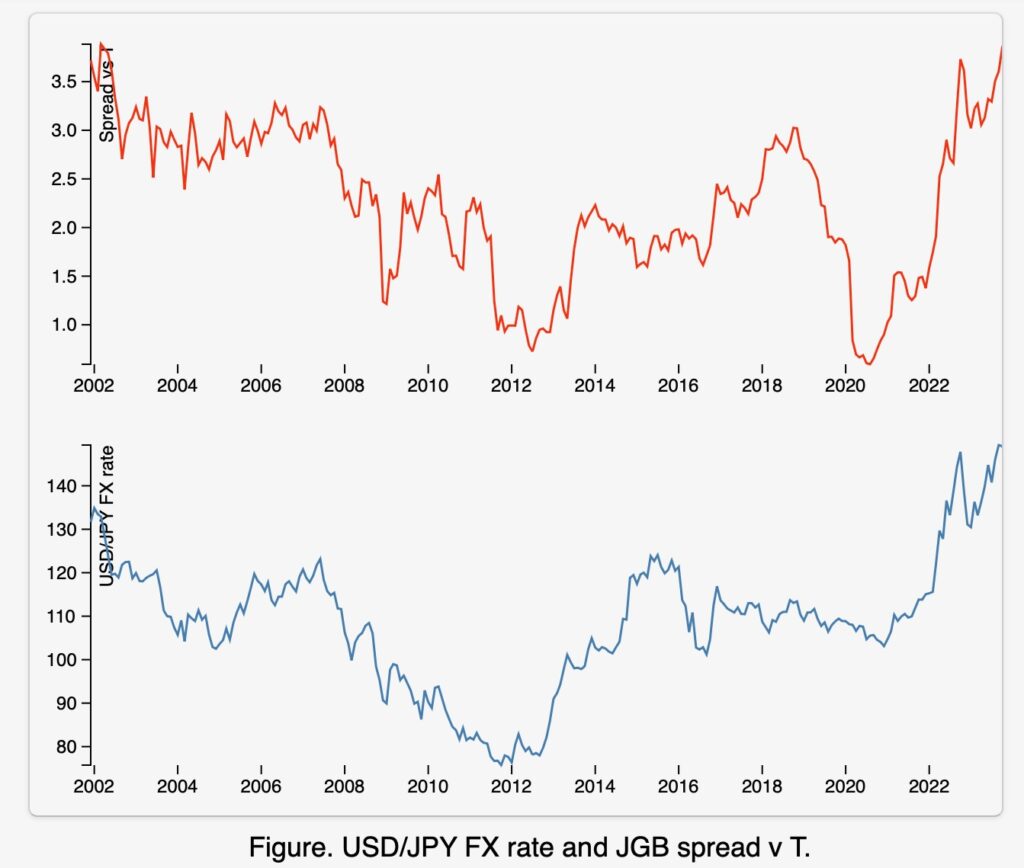
以下の図6は両者のデータをプロットし、線形的な従属性を示したものです。X軸が金利差、Y軸がUSD JPY為替レートを示しています。
図6 日米長期金利差とUSD JPY為替レート
潜在変数(交絡因子)の追加
リーマンショックを契機としたサブプライム・ローン危機による金融不安、その後の欧州における、ギリシャの財政問題を契機とした欧州債務問題による金融不安、この期間をグローバルなliquidity Riskとみなし、Liquidity RiskによるRisk要因を交絡因子と見做します。FRBが金融緩和政策をとり、その後ECBも大規模な緩和政策を取りました。Liquidity Riskが上昇した場合、政府による金融緩和政策が取られ、流動性供給の結果、ドル円レートに影響が出ると同時に、消費支出が減少し、CPIにも影響します。
金融不安定性が高い時、(Minsky moment )Liquidity Riskが高い場合、USDJPY為替レートは上昇トレンドが生じ、消費を控える結果、CPIの上昇は鈍化するか下落傾向に転じます。
これをDAGで示したものが図7です、さらにこのデータセットに非線形な関係があり、潜在的な交絡因子を含んでいることを仮定します。
図7 流動性リスクを潜在変数に仮定した構造グラフモデル
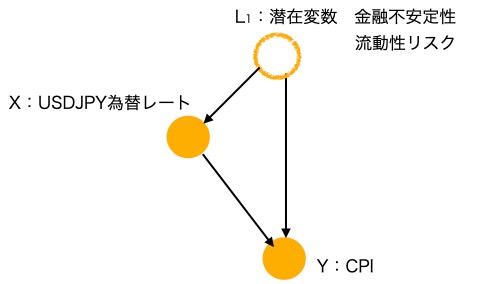
図5を参照すると、USDJPY為替レートが、2018年に急変後にトレンドが転換しますが、これもUS側の事情によるものです。トランプ政権で対中国貿易赤字に焦点が当たり、相互に関税の応酬があった影響です。対米、対中国向けの貿易が大きい日本も影響を受けます。この時はレアアースの資源に関する安全保障上の問題も持ち上がっていました。CPIの上昇基調は、ここでは供給不安の影響と考えられます。
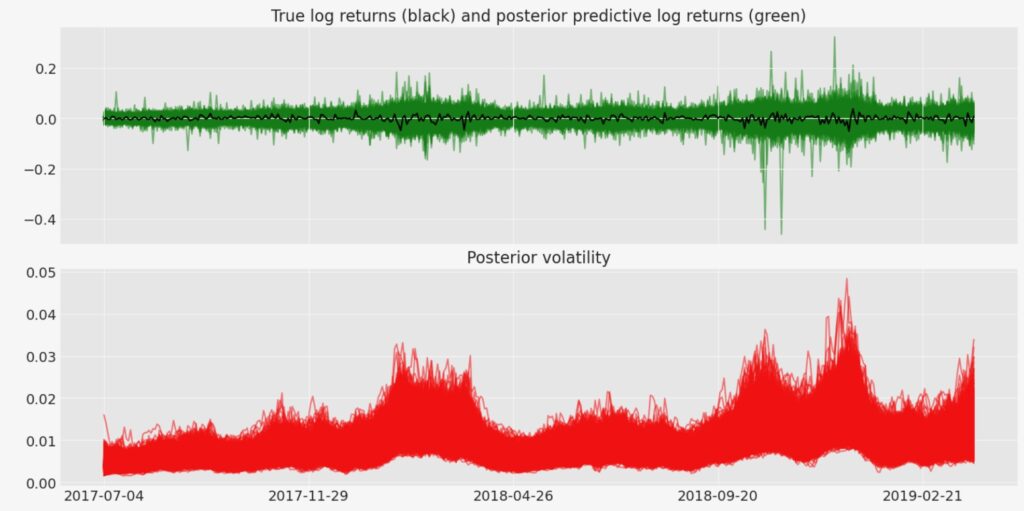
下の図8は、当時2018年以後の株式市場における米中貿易摩擦の影響を示しています。ボラティリティーが上昇しているのがわかると思います。ドル円為替レートもトレンドが転換します。
図8 金融市場のシステミックリスクの伝搬による株式市場のボラティリティーの上昇
非線形モデル
ここで図7のDAGで示したモデルをシミュレーションした、交絡因子にliquidity riskを仮定し、USDJPY為替レートを変数にしたCPIの非線形モデルです。
以下の図9は、これをモデル化して生成した合成データをプロットしたものです。
CPIと為替レートの非線形モデルによるシミュレーション結果です。Rを使ってシミュレーションしています。
このモデルでは、CPIがゼロ以下で、継続して物価が下落している状況を赤のドットで示しています。スロープは通常のグローバル経済(主要国の)が金融システムと経済活動が安定している状況を示す青のドットより、為替レートへの反応を示すスロープ緩やかになります。
2008年以後のサブプライム危機による金融システムの不安定製と流動性リスクの上昇、2010年以後の欧州債務危機による金融の不安定製と流動性リスクの上昇を反映したものです。
金融不安時は数年に渡り、ドル円為替レートの上昇トレンドが継続します。欧州債務危機に対する流動性供給により、赤い点で示すようにCPIはゼロ以下でデフレーションの状態にあります。この間ドル円為替レートも円高が進行します。この円相場の下落局面を過ぎるとNormal状態に戻り、CPIとの間で、緑の点で示す関係に入ります。
図9 非線形モデルによるシミュレーション

冒頭で示したCPIと為替レートの推移のデータセットが、二つのクラスのデータの塊からなることを仮定し、流動性リスクを潜在変数として追加し、CPIと為替レートを非線形な関係としてモデル化し、シミュレーションした結果です。ゼロ以下のCPIのデータの挙動を適合させています。
備考: ガウス過程
ガウス過程は、平均関数と適当な共分散関数によって完全に定義されるため、分析を行う上で便利です。
ガウス過程では、任意のデータの同時分布が多変量正規分布となります。この場合、空間的予測分布の計算が容易になりモンテカルロシミュレーションのサンプリングが実行できます。
ここで使用しているデータセット、CPIと外国為替レートの関係にガウス過程が適用できるかは検討の余地があります。ここで取り扱っているデータセット(x,y)はiidではありません。1
データセットがガウス過程を満たすを確率過程であれば、以下で示す種類の予測が使えます。
ブラックボックス・スタイルの予測モデルのサンプルとしてガウス過程でモデル化します。この方法は、どのようなデータの変数モデルにも一致させる必要なく使えます。
新しい入力x∗に対する予測y∗を予測します。
p(y1,...,yN,y∗|x1,...,xN,x∗) = p(Y,y∗|X,x∗) この分布が、ガウス過程と未知の関数f(x)が両者の関係を示すと仮定した時、入力データからモンテカルロシミュレーションにより事後分布を計算し未知の関数を推定します。
事前分布にガンマ関数を指定します。観測値はノイズを含んでおり、事前分布はノイズパラメータの自由度を割り当てます。
多くの機械学習アプリケーションは、データ生成過程の背後にある本当の基礎となるメカニズムについての知識は限定されています。ガウス過程フレームワークの利点は、関数の数学的なスムージングについてよくわかっていることです。
ここでは未知の関数f(x)のスムージングのためだけに使っています。観測されていない両側の値(円安、円高方向)の為替レートを入力してのCPIの予測は想定していません。
図10にモンテカルロシミュレーションの結果だけ示します。
図10 ガウス過程によるモンテカルロシミュレーション
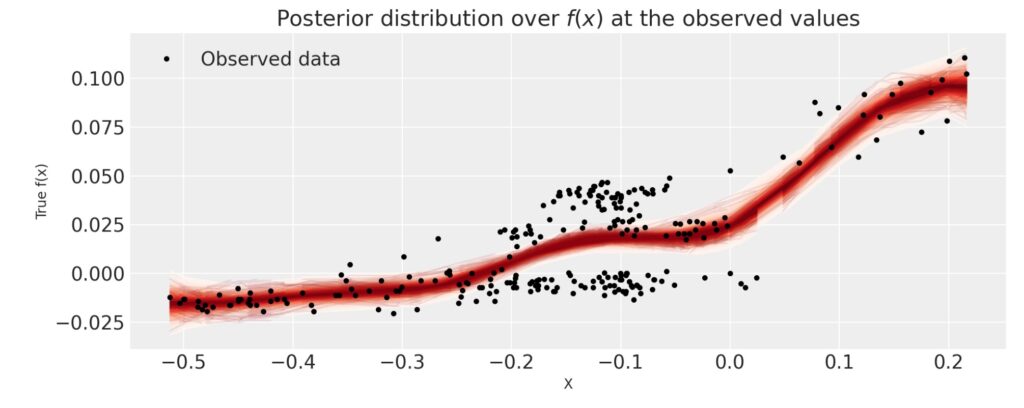
観測されていない点における予測では、観測データを所与とする条件付き分布が用いられます。
この場合、条件分布を追加することで、新しい値を予測することができます。
- xに時間軸をとれば自己回帰モデルとして、この確率過程を適用することもできます。 ↩︎