合理性の限界について検討を重ねていたハーバート・A・サイモンの時代は、ダニエル・カーネマン氏等の行動ファイナンスは経済学の主要な流れとはなっていませんでした。
サイモンは複雑系経済学の起源の一つとみなせますが、その時は複雑系という用語もありませんでした。 サイモンは人工的な現象(経済現象を含む)は、環境に従順であるという点で”環境依存性”を持っているとみなしていました。
サイモンの仕事を継承するような、現在、複雑系や行動心理学の分野で活動している人々は、不確実な状況での認知や予測に関して新しい知見を提供しています。
市場経済における資産管理では、基本的な統計手法としてシャープレシオ、裁定価格理論(Arbitrage Pricing Theory:APT)や平均・分散アプローチによるモダンポートフォリオ理論(Modern Portfolio Theory: MPT)などの手法が提案されてきました。
マーコヴィッツのポートフォリオ理論に基づくポートフォリオのパフォーマンスが、ヒューリスティックによる単純な均等な割り当てのポートフォリオにパフォーマンスで劣るケースが発生することがあります(注1)。
なぜでしょうか。
ヒストリック・ボラティリティーやシャープ・レシオは過去の履歴に基づくため、将来も統計的に同じように振る舞う場合は、過去の履歴に基づく選別は正しいでしょう。自己回帰モデルが適用できるようなケースに相当します。
実際は、将来は過去の延長ではないため、回帰分析やヒストリカル・ボラティリティーでの将来予測は限定的な推定になります。
マーコヴィッツのパフォーマンスが必ずしも最適ではないのは不確実性のためです。
モダンポートフォリオ理論(MPT)を振り返ってみましょう。
モダンポートフォリオ理論
分散投資(diversification)の概念は、収益率の期待値としての確率分布の平均、リスクとしてのその確率分布の分散を用いることで、リターンとリスクを統計的に客観的に取り扱います。
ハリー・マーコヴィッツの提案するMPTはポートフォリオを生成するために平均分散アプローチによって、最小のリスクで最大のリターンを生成するように最適化したものです。MPTは与えられるリスクレベルで期待リターンを最大化させるポートフォリオをどのように構築するかを説明しています。
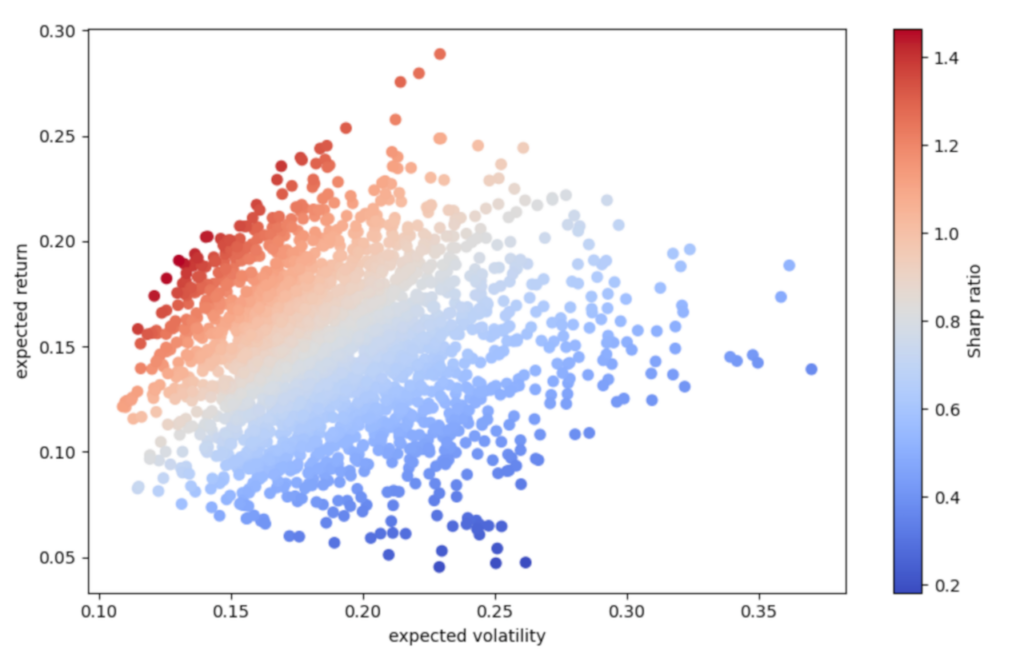
図1 はNasdaqに上場されているいくつかの銘柄を基にモンテカルロシミュレーションで作った擬似的なランダムポートフォリオの期待リターンとボラティリティーを図示したものです。シャープ・レシオを赤から青のグラデーションの色で識別できるように表示しています。
濃い赤字を結んだ曲線が効果的フロンティア(efficient frontier)になります。所与のリターンの水準でリスクが最小であるポートフォリオです。
図1 リターンとボラティリティーの分布
過去の履歴に基づくボラティリティーやシャープレシオは、対象となる資産価格の時系列データの期間の取り方で値が変化します。
以下の図は、ロンドン証券取引所(LSE)の上場銘柄に関して、ある時期の大小、異なる期間の期待ショートフォールとリターンを図示したものです。縦のY軸がリターンの平均、横のX軸がボラティリティーの代わりに期待ショートフォールを示しています。図2は長期、図3は中期、図4は短期のデータから導出しています。
図2 LSE リターンと期待ショートフォール(長期)
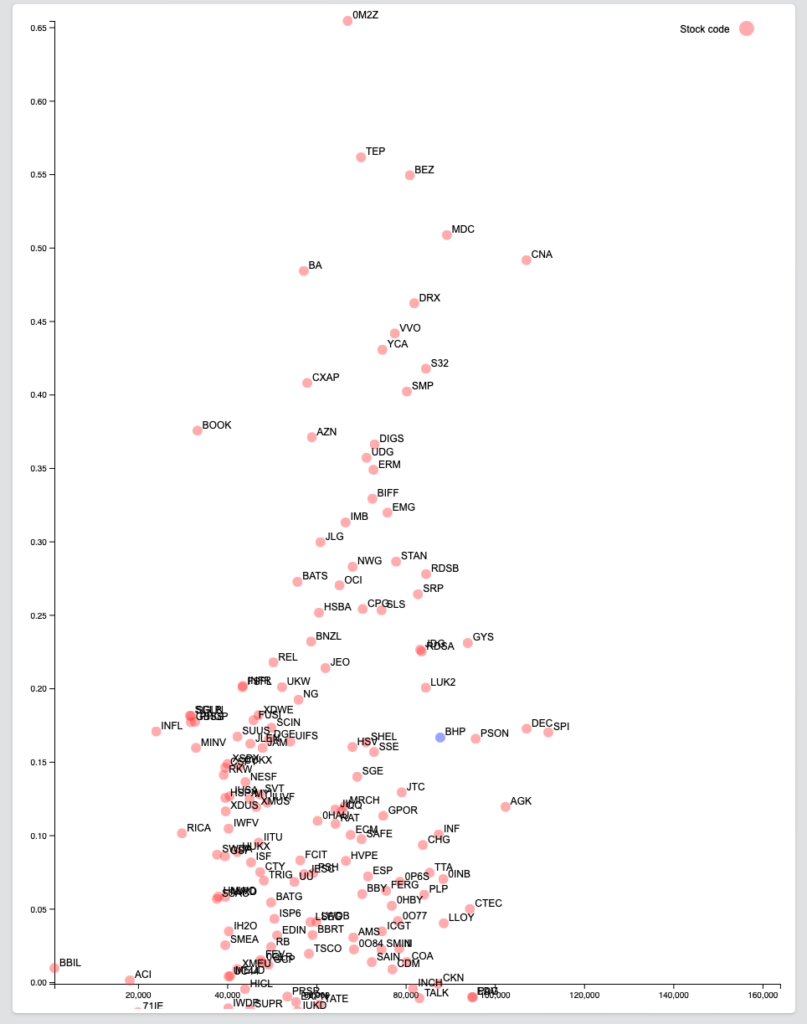
図3 LSE リターンと期待ショートフォール(中期)
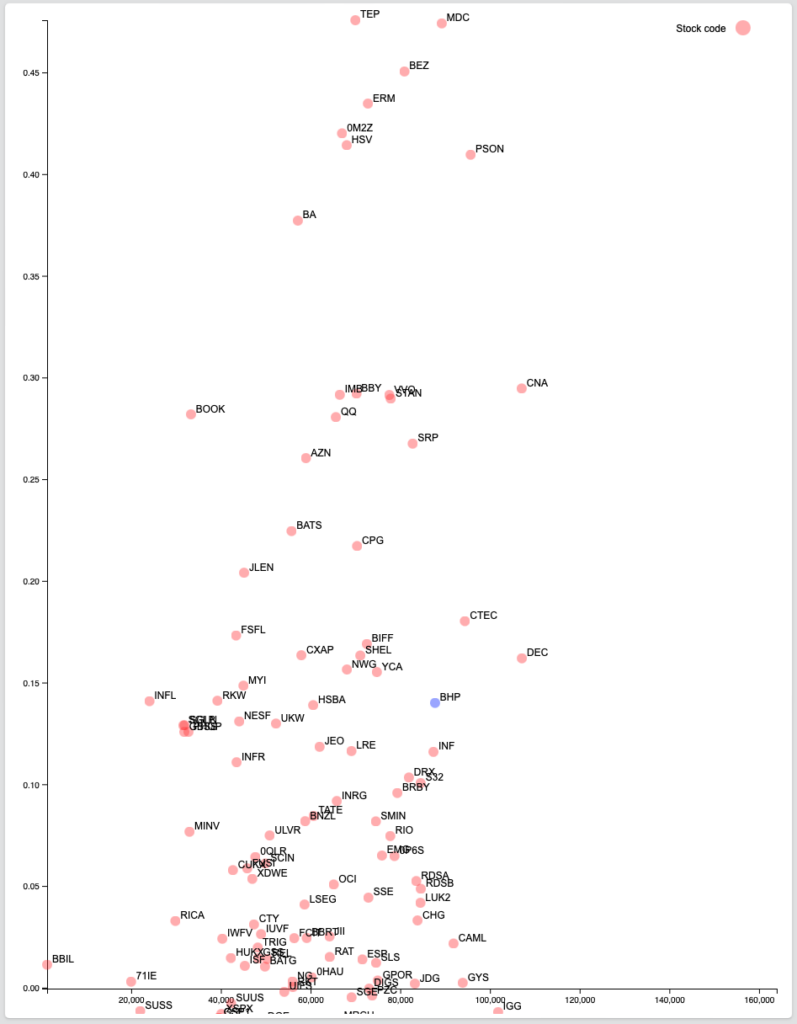
図4 LSE リターンと期待ショートフォール(短期)
高いリターンと低いボラティリティーを示す銘柄は、その時点からの過去に遡る期間のサンプルデータの取り方で変わります。これは、過去の一定期間の結果が、将来の同期間のリターンとボラティリティーの関係を示すことを約束するものではありません。
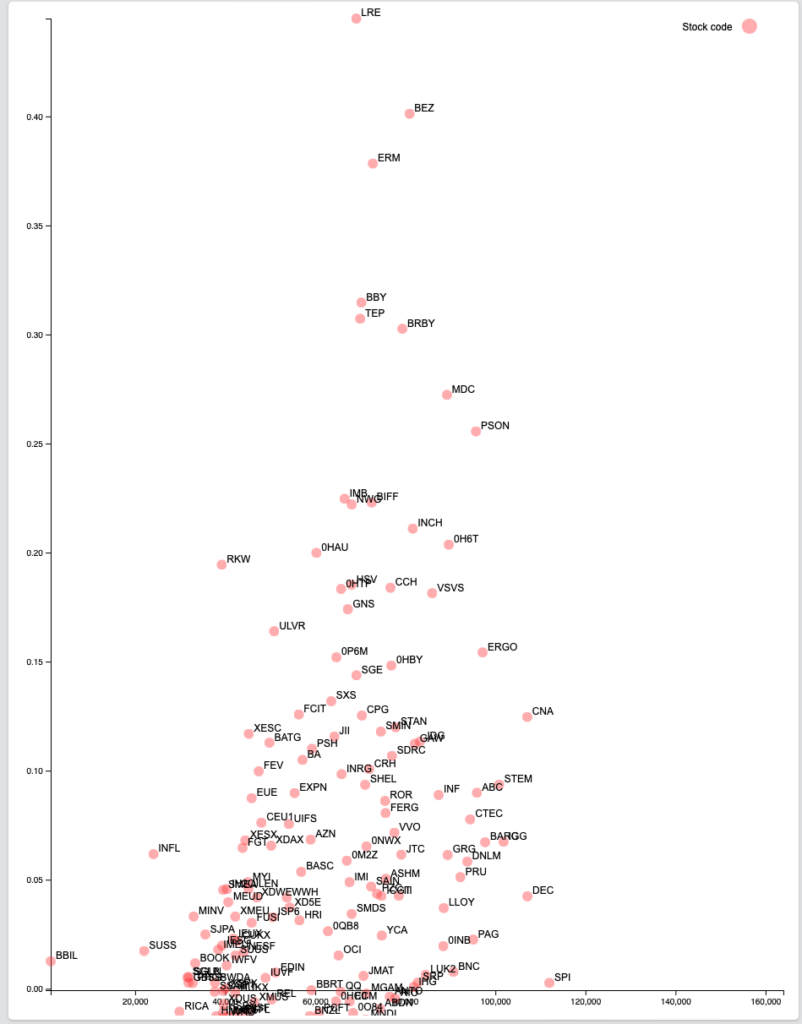
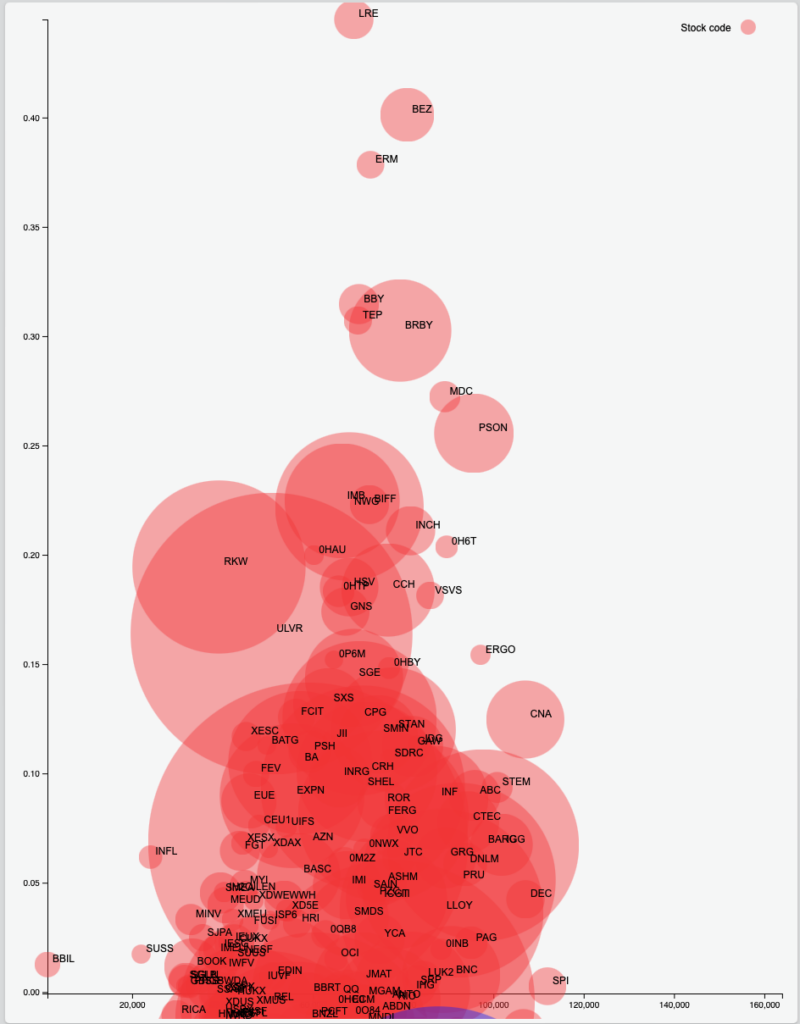
図5は図4と同じデータセットですが、円の大きさがその期間の日次の出来高の平均、流動性を示しています。
青のマーカーで示した銘柄BHPを例にとると、図5の短期のリターンの平均はマイナスになっており、円の上部だけを表示しています。タイムスパンの取り方によって統計データの示す内容は変化します。
図5 LSE リターンと期待ショートフォール、 流動性(短期)
平均・分散アプローチは、回帰分析同様、将来も統計的に同じように振る舞うという仮定の上で予測に使うことができます。リターンの平均、期待ショートフォールのような過去の履歴に基づくデータは有用です。当該指標を含めて、どのようなリスクモデルや指標を判断材料とするかは意思決定者によります。
MPTが将来のベストなポートフォリオを示しものではないことは明白です。とはいえ統計的な処理が無意味であるかというと、決してそうではありません。不確実性の度合いの問題です。
多くの経済学では合理的な判断をする人間を前提に、理論を構築しています。複雑系の概念を基に調査しているジェームズ・ドイン・ ファーマー氏は、合理的な意思決定をする個人の集合体ではなく、不合理に行動する行為者(エージェント)のアンサンブルを用いた経済システムでシミュレーションを行なっています。
ファーマー氏はカオスの研究者でしたが、システムの初期の揺らぎがその後に大きく影響するというバタフライ効果はよく知られています。これは初期のカオティックな挙動がその後のシステム全体に影響することです。常にこうした挙動が増幅されるのであれば、回帰分析自体が意味のないものになります。
そうした不確実な状況は、特別なものでなくありふれて発生します。情報伝達においてはエントロピーの逆数が情報量として定義されます。元データに乱雑さが混入することで、伝達先では、元のデータが変化します。

因果の探索においては、観測データから元の因果の構造を探索します。一部の因果の構造が既知であれば、事前情報として探索アルゴリズムに与えることができます。
株式市場などの金融市場において、因果の構造が明らかであれば、予測に役立てることができます。
現代の市場を通じた経済システムは、国際間で統合されて影響を及ぼしあう傾向があります。CPI等で評価されるインフレーションも、FTAの推進と国際間の貿易量の拡大に伴い国際的な統合が進展している面があります。先進国ではインフレーションや市場価格は伝播するため、エネルギーなどの一次産品の国際取引を通じた国外依存度の高い国では、一国の経済政策だけで完全に制御できるものではなくなっています。
原因が自国に依存していない場合、つまり外因によるインフレーションに関しては、自国の経済政策で対症的な対応は可能ですが、直接その契機となった原因を取り除くことは外部への働きかけと影響力の行使が必要になり、必ずしも自国の都合で取り扱える範囲にはありません。これは他国に伝播していれば、その影響がさらに相乗的に影響してくる程、先進国では貿易の仕組みや金融システムを通じて経済システムが統合されていれます。
平均分散アプローチによるMPTを基にしたポートフォリオも不確実性の度合いによっては、最小のリスクと最大のリターンの組み合わせとなりません。これは過去のデータへの適合が将来の予測の精度につながらない状況です。
リスク(知られているリスク)と不確実性(知られていないリスク)を取り扱う手法として、期待ショートフォール他、たくさんの統計的なリスクモデルがあります。その多くは、過去の履歴を基にしたものです。過去の履歴だけでは軍事侵攻から発生する影響は予測できません。このような突発的な出来事に対するリスク管理の手法もあります。
図6 VaR に対して、Fat Tailなリターンの分布に対応した期待ショートフォール
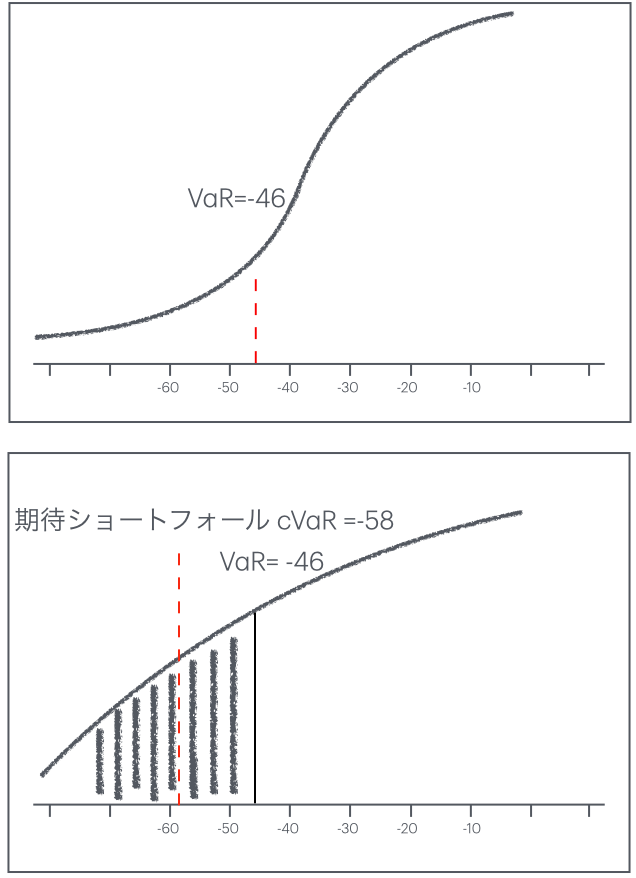
地政学的な出来事が発生するような状況では、市場の振る舞いは過去の履歴から乖離します。
ファーマー氏は、モデルの評価に際しては、過去のデータに適合することよりむしろ、その将来の予測に注目することであると主張しています。
機械学習の分野では過去のデータに適合させてモデルを作成し、モデルの精度を測りますが、予測に対しては、過去のデータに過度に適合することで、将来の予測の精度が低下することは、過学習(over fit)としてよく知られています。
データからモデルをバックテストする場合、ブートストラップやクロス・バリデーションの手法が取られます。
ブートストラップは、パラメータを推定する際に限定されたデータからサンプリングデータをシミュレーションして、テストする手法で元データに依存したデータが生成されます。
クロス・バリデーションは、モデルを検証するための再サンプリングの手法です。元データをあらかじめ学習用とテスト用のデータセットに分離し、学習用データでテストしたモデルの精度をテストデータで検証します。
どちらの手法も生成されるモデルの性質は、元データに依存します。
既知の情報の上でシミュレートされたポートフォリオ、不確実性の上で成立する生成ポートフォリオと未知の結果は常に異なります。
エコロジカル(生態学的)合理性
不確実性下での判断は、ヒューリスティックスがより正確な予測をする場合があります。
従来のヒューリスティックスの考え(注2)では、ヒューリスティックな意思決定は、統計的なモデルや論理に従う合理的な判断より、大きな誤りを招くと見られていました。
心理学者のGerd Gigerenzer氏等は、単純なヒューリスティックスが、より情報量の多い統計的な手法よりもっと正確なケースがあることを見つけています。これ等の結果は’less-is-more effects’として知られています(注3)。彼らは 正確さと情報、計算、時間の量との間に逆U型(inverse-U-shaped)の関係があると主張しています。
こうしたヒューリスティックな判断が、より洗練された統計的な手法より、高い予測精度を上げる理由は、以上、述べたようにサンプルデータへの依存度と不確実性です。モデル化に際しては予測のベースになるデータの性質について、正しく把握しておく必要があります。
ブートストラップやクロスバリデーションのような統計的な手法もサンプリングされた状況や条件に元データの性質に左右されます。心理学の"less-is-more effects"や機械学習におけるover fitのために、現実の世界で予測モデルよりヒューリスティックな判断の方が良い結果となる状況は起こります。それにもかかわらずデータサイエンスが有効であるのは、客観性のある尺度を提供できることにあります。
Gigerenzer氏らは、ヒューリスティックスに関してシステマティックな理論の構築を試み、異なる状況に対応した問題解決のためのツールボックスを提案しています。
なぜヒューリスティクスが有効であるか、Gigerenzer氏は二つの回答を用意しています。精度に対する労力のトレードオフと、ヒューリスティクスの生態学的合理性(ecological rationality)(注4)です。
生態学的合理性とは、ヒューリスティックスは、環境の構造に適応する度合いへの生態学的な合理性であるとする、新しいフレームワークです。ヒューリスティックスは良い、悪い、または合理的、不合理でなく、その精度が環境の構造に依存するという考え方になります。
この考えは、ハーバート・A・サイモンの'Bounded Rationality'の流れを受けたものです。’サイモンのハサミ’のアナロジー(注5)の新しい取り組みとみなせます。これは、人間の合理的な行動は、ハサミの形を持っており、その二つの刃は、タスク環境の構造と、行為者の計算能力であるというものです。片方の刃だけを見ていると、認知について、あるものは、なぜ、いつ失敗、あるいは成功するか理解できません。
合理性は内部の基準に依存するだけでなく、環境の構造にも依存します。
環境の構造とは、(Todd 2011)以下の項目を含んで識別されます。
- 不確実性
- 冗長性:刺激(cue)間の相関
- サンプルサイズ:観測値に関する
- 変数の重み:刺激の重みの分布
これはコンピュータサイエンスで、より洗練された学習アルゴリズムとしてreinforcement learning に通じます。ニューラルネットワークの変数は各ニューロンの重みづけなので、外部刺激の入力で学習が進みます。心理学と機械学習という別の分野からの取り組みですが、手法が同じアプローチになっています。生態学的合理性(ecological rationality)は、reinforcement learningと共通点の多い概念です。
生態学的合理性において鍵となる問題は、複雑な環境に組織を適応させることです。単純なタスクを例にとると、階段を上るタスクでは、重要なのは階段を上ることを管理することで、階段の登り方がわかることではありません。これはニューラルネトワークを使った機械学習と同じ考え方です。
Brunswik氏やGigarenzer氏らは、これは経済にとっても極めて重要であるとみなしています。タスクをアーカイブするためには複数の多重の方法があることが明らかになっています。Gigarenzer氏らは、重要なストラテジーとして、それにヒューリスティックを使うことを試みています。
注:参考資料
- Alain Samson. “The Behavioral Economics Guide 2015”
- Tversky & Kahneman "Judgment under uncertainty: heuristics and biases." 1974
- Gerd Gigerenzer, Wolfgang Gaissmaier "Heuristic Decision Making", 2011 by Annual Review of Psychology
- Gerd Gigerenzer, "Ecological rationality: Intelligence in the world."
- Herbert A. Simon “Invariants of Human Behavior” 1990 Annual Review of Psychology