do-Calculusの概念を解説します。do-演算子(do-operator)と条件確率式で定義してあり、PearlのDAGを元にした因果推論の中心的な概念です。d-Calculusの三つのルールはd-separatorという概念を適用することで、ある確率分布が別の確率分布と等しいことを示すものです。直感的に把握するのは難しい概念であるかもしれません。DAGをイメージして把握した方が良いでしょう。
DAGで示した確率空間でノードの数が少なくなれば、同時確率分布、条件確率分布において計算が簡素化できます。
ブログポスト”投資ポートフォリオのストレス・テスト”において、第3の変数によって"シンプソンのパラドックス"が起きることを説明しました。do-Calculusは、このパラドックスを避ける方法です。
本稿ではdo-Calculusを解説した後、前述のブログポストのシナリオの例を使って、シナリオの結果としてのポートフォリオの損益を推論します。これは構造化因果モデルを使ってcounterfactual推論の結果を計算することになります。
do-Calculus
do-Calculusのルールを以下に示します。
ルール1 (観測値の挿入と削除)
\[ P(y | do(x), z, w) = P(y | do(x),w) \]
\[ if (Y \perp Z | X,W) _{G_{\bar{X}}}\]
ルール2(観測値と介入の交換)
\[ P(y | do(x), do(z), w) = P(y | do(x),z,w) \]
\[if (Y \perp Z | X,W) {_{G_{\bar{X} {\underline{Z}} } }} \]
ルール3(介入の挿入と削除)
\[ P(y | do(x), do(z), w) = P(y | do(x),w) \]
\[if (Y \perp Z | X,W) {_{G_{\bar{X} {\bar{Z(w)}} } }} \]
これはバックドア基準(後述)に関連した共変量の選択の問題です。
以下、4つの変数について考えます。
- Y:結果
- X:処置
- Z:ルールを適用する第3の変数
- W:交絡因子
前述のブログポストのシナリオに準じて、以下のように簡素化したシナリオを想定します。
- W:交絡因子:社会的、経済的な状況、例えば労働市場の需給状態
- X:FEDの金融政策決定を示すバイナリの選択(1:利下げ、0:現状維持)
- Y:結果としての資産価格、株価
- Z:一次産品価格(原油価格)
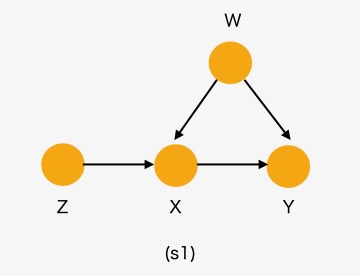
図1 シナリオ
do-Calculusルールは、DAGを簡略化してノード数を減らすために設定されています。ルールを適用するか介入操作(intervention) do(.)を処置することによって、因果の影響を簡素化していきます。
DAGのブロック 確率分布の要素化
実際のルールと介入(intervention)の詳細を見る前に、DAGで示す確率空間での三つのノードの関係について整理しておきます。
異なるグラフの経路を通って相関がどのように流れるかに注目します。DAGでは矢印が因果の方向を示します。
グラフのノードを結ぶ相関の流れの経路として、三つの異なる経路があります。三つのノードが与えられると、以下の3種類の経路のいずれかのタイプが適用できます。
連鎖 chains(→.→)、分岐 forks(←. →)、合流 collider(→.←)
以下、3ノード、X,Y,ZからなるDAGの経路を考えます。
- X:処置
- Y:結果
- Z:第3の変数
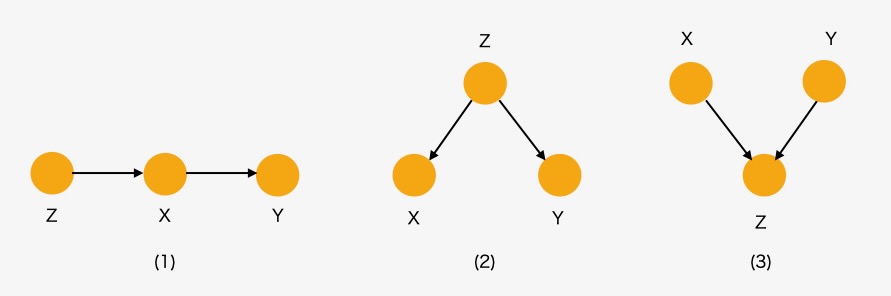
図2 DAGの経路
(1) 連鎖DAG (Chain)
Z→X→Y、Z←X←Y
Yの分布に関して、Xの値だけを知る必要があります。
\(P(Y | X,Z) = P(Y | X)\)
これは、条件確率 Xに関してYとZが独立であることを示します。
\(Z\perp Y | X \)
ZがYと独立であるため、do(.)演算子(Xへの介入intervention)によって、Zの影響を消すことができます。
(2) 分岐DAG(Fork)
X←Z→Y
このケースでは一般的に、多くの擬似相関(偽の相関:spurious correlation)にみられるように、X,Yは独立していないように見えるかもしれませんが、Zが与えられるとXはYに依存しなくなります。
\(P(X | Z,Y ) = P( X | Z) \)
これは、条件確率、XとYは与えられたZの条件で独立であることを示します。
\(X \perp Y | Z \)
ここではこの構造を"交絡(confounder)"でなく、"分岐(fork)"と呼んでいます。すべての"分岐"が"交絡因子"であるわけではありません。以下の図3の構造で、Zは"分岐"ですが、X、Yの交絡因子(confounder)ではありません。
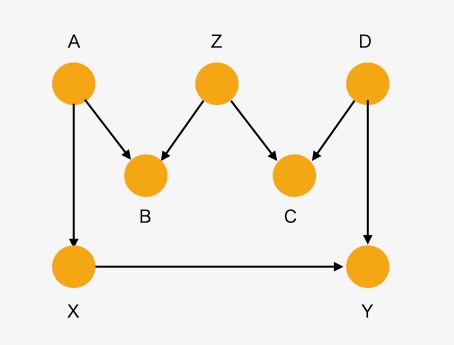
図3 M構造
(3) 合流DAG (Collider)
X→ Z ← Y
XとYはすでに独立しています。変数Zの条件がXとYの独立を妨げることはありません。Zは、X,Yをブロックしていると表現します。Zを条件とするとき、新しい相関(例えば、Z=X+Yのような関係性)の経路が開きますが、XとYは独立したままです。
d-separation
上の図2の(1),(2),(3)、三つの関係をd-separation、Zをd-separatorと呼びます。(d-separatorのdはdirectionalのことです)
d-separationの定義は、変数Zが、X,Yからd-分割(d-separation)、またはブロックすることを意味します。Zの変数の条件によって、XとYの間のすべての相関を切断します。
(2),(3)のケースでは、X、Yの関係が条件Zに関して独立していることを意味します。この関係は、\(X \perp Y | Z \)を示します。
(1)では、X、Yの間に因果関係がありますが、Z、Y間では、Xを条件とした場合、ZとYは独立になります。\(Z\perp Y | X \)
グラフにおいて、ZによってXとYが分離される(separated)ときは、Xは与えられたZによって、Yと独立しています。
ZがXからYへの経路の全てをブロックする場合、"XとYはd-separate"と言います。その時、XとYはZを条件として独立しています。\(X \perp Y | Z \)と表記します。
do-Calculusルールの詳細
4つのノードからなる因果ダイアグラムのケースに戻ります。このダイアグラムを通してdo-Calculusのルール適用に関する詳細を見ていきます。
ルールの適用は、do(.)演算子の処置により、ノード間の矢印(因果関係)を削除することを意図しています。それは、二つのノードの間を因果関係がない状態にし、ノード間の因果の影響の計算を簡素化することです。
これは、3つの推論ルールからなり、因果ダイアグラム内のd-separation条件がある場合に、介入(intervention)と観測値の分布を同じものとみなすことができます。
各ルールには、条件式が定義されています。do-Calculusを把握する上で、重要なポイントなので、以下にまとめておきます。因果グラフ空間Gのサフィックスの変数名の上下にある線の意味が重要です。
- \({G_{\bar{X}}}\) のような変数名の上側に線がある場合は、因果グラフGからXに入力するすべての矢印を削除することで得られるグラフを意味します。
- \(G_{\underline{X}}\) のようにサフィックスの下側に線がある場合は、因果グラフGからXが出力するすべての矢印を削除することで得られるグラフを意味します。
- \(Z(w)\)は、どのようなZもWの祖先(ancestor)ではないZノードを意味し、\({G_{\bar{Z(w)}} } \)のように\(z(w)\)の上側に線がある場合、ZがWの祖先(ancestor)ではないときに、因果グラフGからノードZへ向かうすべての矢印を削除して得られるグラフを意味します。
(1)ルール1 観測値の除去
どのような経路からも結果に影響しないならば(つまり、観測値が結果からd-separatedされるならば)、観測されるノードを無視することができます。定義は最初に記述したように
\( P(y | do(x), z, w) = P(y | do(x),w) \)
if \( (Y \perp Z | X,W) _{G_{\bar{X}}}\)
ここでは、第3の変数としてZに着目しています。Zを削除できるかどうかです。
Xに入力してくるZの矢印を消去して、与えられたW、Xにおいて、YとZが独立したものであれば、Zの変数を削除することができます。Xへの入力を削除した時、YとZがd-separatedであれば、Zは無視できます。
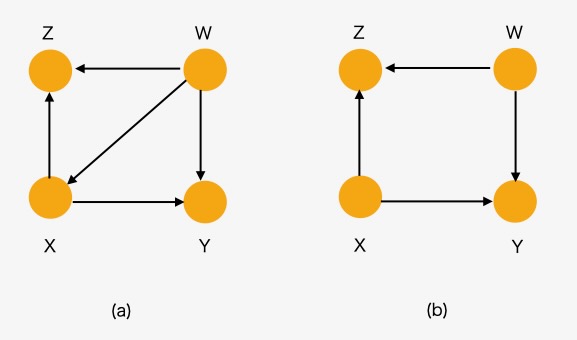
図4 ルール1
do(.)操作によってXの値を固定すると、Xへのすべての入力が削除できます。DAGの構造は図4(a)から図4(b)のように直接Xへの入力は削除され、YとZはd-separated になり(\(Y \perp Z | W,X)\)) W,Xの条件でYとZは独立になります。
こうして、結果Yへの因果の影響からZを削除することができます。
pythonのライブラリpgmpyを使って確認してみましょう。pythonのライブラリをロードします。
from pgmpy.models import DiscreteBayesianNetwork
from pgmpy.inference import VariableElimination
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import CausalInference図4(a)の因果モデルです。
model_a = DiscreteBayesianNetwork([("X", "Y"), ("X", "Z"), ("W", "Z"), ("W", "Y"),("W","X")])
model_a.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()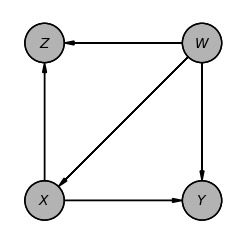
モデルのノード間の独立性を出力します。
model_a.get_independencies()(Z ⟂ Y | X, W)図4(a)からXへの入力を削除したダイアグラムが次のモデル(b)です。
図4(b) のモデルを表示させます。
model_b = DiscreteBayesianNetwork([("X", "Y"), ("X", "Z"), ("W", "Z"), ("W", "Y")])
model_b.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()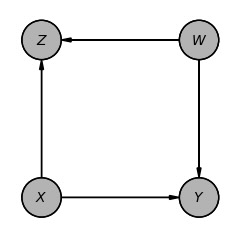
条件独立性を確認してみます。
model_b.get_independencies()(Z ⟂ Y | X, W)
(X ⟂ W)(2)ルール2 介入(intervention)を観測値として扱う
do(z) によって、観測値と一致するのは、zからの出力が結果に影響しない場合です。条件として与えられたX,Wに関してYとZがd-separatedであれば、ZからYへの直接の経路はありません。
条件式の\({G_ {\underline{Z}} } \)は、元のDAGのZの出力全てが除去されることを意味してます。Zの出力とXの入力を除去した時に、ZとYがd-separatedであれば、do(z)を観測値として処理できます。
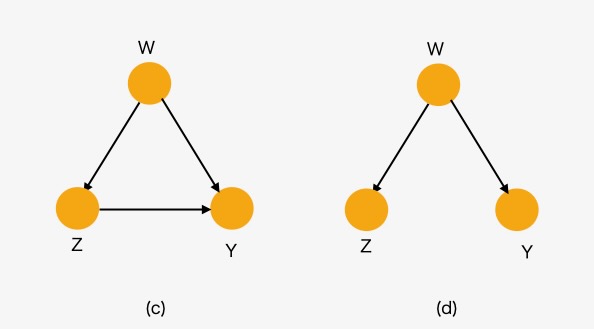
図7 ルール2 モデル(c), (d)
上の図7(c),(d)は、3変数の場合です。Zの出力を削除した場合、Z,YはWに関してd-separatedになります(\(Z\perp Y |W\))。
model_c = DiscreteBayesianNetwork([("W", "Z"), ("Z", "Y"), ("W", "Y")])
model_c.to_daft(node_pos={"Z": (0, 0), "Y": (2, 0), "W": (1, 1)}).render()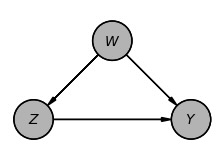
model_c.get_independencies()model_d = DiscreteBayesianNetwork([("W", "Z"), ("W", "Y")])
model_d.to_daft(node_pos={"Z": (0, 0), "Y": (2, 0), "W": (1, 1)}).render()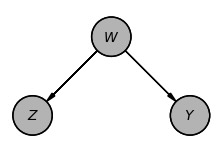
独立性を出力してみます。
model_d.get_independencies()(Z ⟂ Y | W)以下、4変数の場合です。
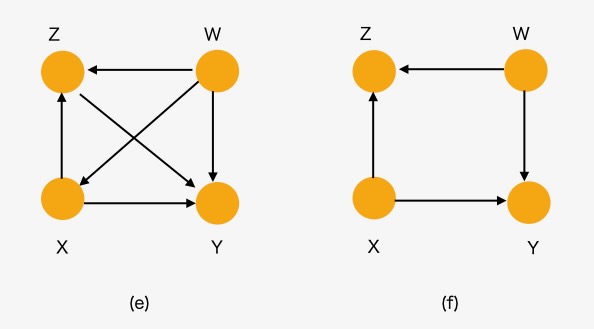
図10 ルール2 モデル(e),(f)
図10(e),(f)の例を参照してください。図(e)にルール2の条件を適用し、ノードZからの出力とノードXへの入力の全てを削除したDAGが図(f)です。この図(f)のDAGは、ZとYはd-separatedになります。( \( Z \perp Y |W, X \) )
このとき、\( P(y | do(x), do(z), w) = P(y | do(x),z,w) \) として、Zに関して介入(intervention)が観測値Zと交換できます。
model_e = DiscreteBayesianNetwork([("X", "Y"), ("X", "Z"), ("W", "Z"), ("W", "Y"),("W","X"),("Z","Y")])
model_e.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()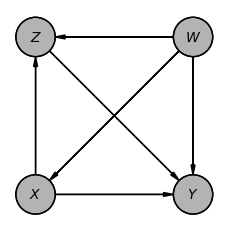
model_f = DiscreteBayesianNetwork([("X", "Y"), ("X", "Z"), ("W", "Z"), ("W", "Y")])
model_f.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()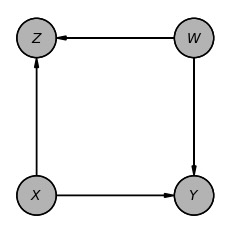
独立性を出力します。
model_f.get_independencies()(Z ⟂ Y | X, W)
(X ⟂ W)(3) ルール3 介入(Intervention)の除去
do(.)演算子の処理した変数が除去されます。これは、どのような経路を経由しても結果に影響しない場合、介入(intervention)の変数を無視することができます。ZからYに対して因果関係がない場合に、do(z)が除去できます。
最初の条件式で示したように、前提として、\({G_{\bar{X} {\bar{Z(w)}} } } \)という条件があります。これは、どのようなZノードもWの祖先ではない事を意味しています。Z → Wの向きに矢印がある場合、ZはWの祖先であるため、この条件には合致しません。ZノードがWの祖先でない場合にのみ、Zノードに入力する因果の経路である矢印を削除することができます。下の図13では(h)のケースに相当します。(g)のケースは、ZがWの祖先であるため、前提条件に合致しません。
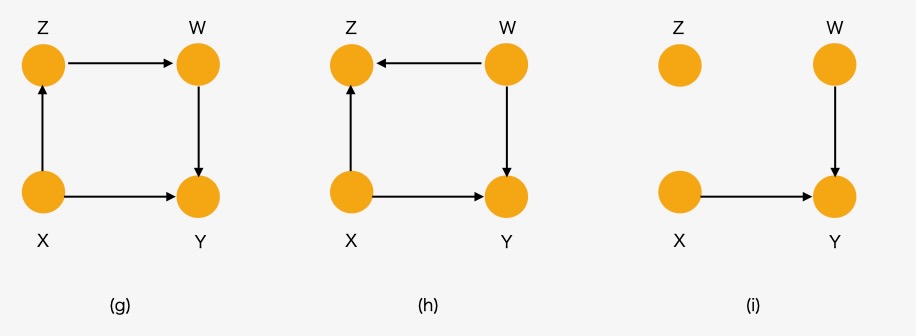
図13 ルール3 モデル(g),(h),(i)
(h)のモデルでは、前提条件に一致するため、Zに向かう矢印を削除することができます。ルール3が適用されて、元のモデル(h)からZに入力する矢印を削除したDAGがモデル(i)です。条件確率分布からdo(z)を削除することができます。
model_h = DiscreteBayesianNetwork([("X", "Y"), ("X", "Z"), ("W", "Z"), ("W", "Y")])
model_h.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()
model_h.get_independencies()(Z ⟂ Y | X, W)
(X ⟂ W)model_i = DiscreteBayesianNetwork([("X", "Y"), ("W", "Y")])
model_i.to_daft(node_pos={"X": (0, 0), "Y": (2, 0), "Z": (0, 2), "W": (2, 2)}).render()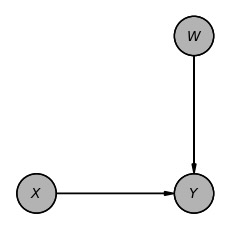
モデル(i)の独立性を取得します。
model_i.get_independencies()(X ⟂ W)以上がdo-Calculusの三つのルールですが、図2(b), 図10(f)、図13(h)は同じ形式の因果ダイアグラムになっています。つまり、最初の図2(a)で示した因果ダイアグラムは、ルール1を適用して図2(b)、または、図13(h)の形式に変換でき、さらにルール3を適用して図13(i)の形式に変換できます。
図10(e)の因果ダイアグラムは、ルール2を適用して図10(f)の形式へ、その因果ダイアグラムにさらにルール3を適用すると、図13(i)の形式になります。
図13(i)は3ノードからなる因果ダイアグラムで、X→Yへの直接の因果の影響を計算することが簡単になります。
因果ダイアグラムがdo-operatorを含まなくなるまで、do-Calculusのルールを繰り返し適用することによって、因果の影響の計算を簡素化することができます。
最終的な式は、
\[P(y | do(x)) = \sum_{w} P(y | x,w) * P(w) \]
最後の図13(i)の因果ダイアグラムは、次項のバックドア基準を示す式と合致します。
バックドア基準
do-calculusが導出する最も強力な結果は、観測値から処置の効果を予測するための変数のセットを特定することです。この変数のセットは、以下の式の変数Zに一致します。
\[P(y | do(x)) = \sum_{z} P(y | x,z) * P(z) \]
Zは、Yに対するXの因果の影響に関係するすべての交絡のバイアスを除去することを保証します。
式の右辺のすべての因子は、介入(intervention)前のデータから推測できるので、因果の効果はそのようなバイアスのないデータから推定することができます。
ベイジアン・ネットワークによるシナリオ分析
図1のシナリオを例に取ります。
Xはバイナリ変数(1または0)とします。FEDの金融政策の変更の有無を示します。
時系列データの処理に関しては、時間Tで発生したイベントの効果を測定するのに、その他の同時に発生している因子の結果への影響は、そのイベントの前後で一定であることを前提にしています。この視点によって、因果の効果を線形回帰で推定することができます。
FEDの金融政策において、FFレートの目標値は、2025年度は4.5%に設定されていましたが、9月、10月の金融政策決定会合で、連続して0.25%の利下げが実施されました。この利下げの決定時の株価データを用いて、利下げの効果を推定します。
| Date | FFレート上限 | 下限 |
| 2025/1~ | 4.5 | 4.25 |
| 2025/9/18 | 4.25 | 4 |
| 2025/10/29 | 4 | 3.75 |
| 2025/12/11 | 3.75 | 3.5 |
因果の効果の推定
結果としての株価のリターン(Y)は、Tの時系列データとして扱います。XをFEDの決定を示すバイナリ変数として扱います。
XからYへの因果の効果 ATE(Average Treatment Effect)は、以下の式で示せます。
\[ ATE = E[Y | do(X=1)] - E[Y | do(X=0)] \]
このATEを計算するのに、平均値を取る方法があります。Xの1と0の場合の結果の平均値の差分を計算します。以下の式で示します。
\[ATE = \frac{1}{{n}_{w+}} \sum _{T\preceq {t} \preceq {T+w}}Y(t) - \frac{1}{{n}_{w-}} \sum _{{T-w}\preceq {t} \preceq {T}}Y(t)\]
\({n}_{w-}\) は、イベントの発生時間Tより前の時間間隔[T-w,T]における観測値の数、\({n}_{w+}\) は、イベント発生後の時間感覚[T,T+w]における観測値の数を示します。
ここでは、Y(t)にポートフォリオの構成資産の資産価格でなく、株価Indexを用います。
利下げが実施された日(政策目標が変更された日)をイベントの発生日 T として、前後の時期における株価Indexの時系列データをY(t)のサンプル値とします。
結果の平均値を計算する上で、イベントTの前後の時系列データのサンプル値の数が十分ではないため、ブートストラップでサンプリングして平均値を計算します。
\(E[Y | do(X=1)]\) は、株価(例としてindex)の処置後、時間Tから時間W後までのブートストラップ値
\(E[Y | do(X=0)]\)は、株価の処置前、時間W以前から時間Tまでのブートストラップ値
サンプリングデータは、イベントTの前後の10日間のデータを元に5000サンプリングしています。
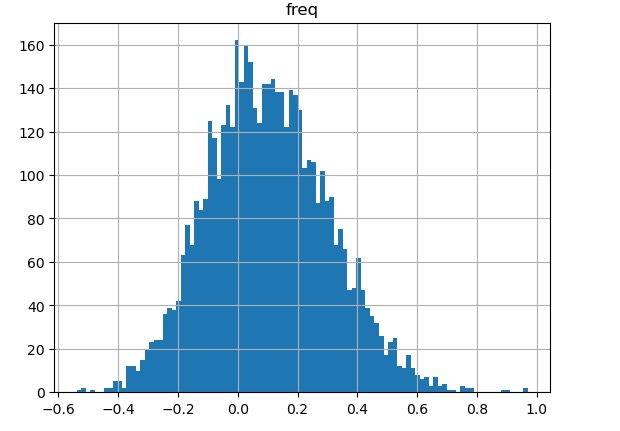
図16 イベント発生前の株価インデックス(DJI)のサンプリング結果
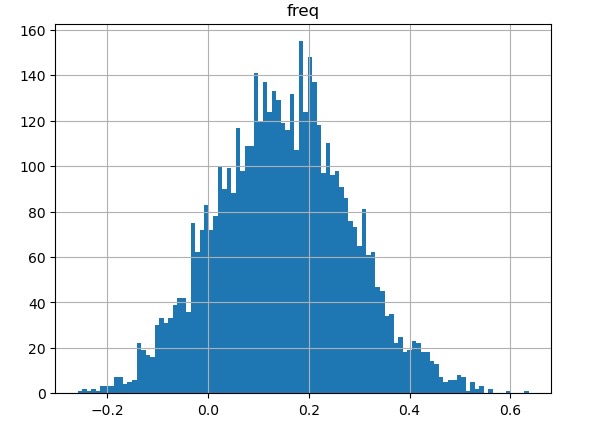
図17 イベント発生後の株価インデックス(DJI)のサンプリング結果
以下のテーブルにブートストラップでサンプリングしたリターンの平均値を示します。
【Dow Jones Industrial Average】
| wサイズ | T-w | Decision T | T+w | 事前平均値 | 事後平均値 | ATE |
| 10 | 9/4 | 9/18 | 10/3 | 0.099861 | 0.144989 | 0.045128 |
【SP500】
| wサイズ | T-w | Decision T | T+w | 事前平均値 | 事後平均値 | ATE |
| 10 | 9/4 | 9/18 | 10/3 | 0.166475 | 0.141379 | -0.025071 |
ATEの値を元に推定する場合、この平均値を用いる方法によると、
.25%の利下げで、株価の期待リターンの期待値がx%下落、または上昇します。
線形回帰の差分
別のアプローチとして、線形回帰の差分を用いる方法があります。
時系列データの線形モデルでは、イベントTの前後の時間を変数にして、二つの線形回帰モデルを考えます。イベント発生時間Tの前の系列と発生後の系列を計算し、それぞれに個別の傾き(slope)と切片(intercept)を計算します。
(1) 出力(株価)をYとして、イベントの発生時間T以前のYの線形モデルは、
\(Y_i | [t<T] = Y_i | [D_i = 0] \)
\(= b_0 + a_0 * t_{i} + \epsilon_{i} \)
時間Tでイベントが発生する前なので、\(D_i=0 \) の場合、切片は \(b_0 \)、傾きは\(a_0\)
(2) イベント発生時間T以後の線形モデル
\(Y_i | [t>T] = Y_i | [D_i = 1] \)
\(= b_1 + a_1 * t_{i} + \epsilon_{i} \)
時間Tで\(D_i\) = 1 が決定された場合、切片は\( b_1 \) 、傾きは\(a_1\)になります。
このATEは図18に見られるように、時間t=TにおけるT以前の回帰における終端(t=T)の値と 時間T以後の線形回帰の切片(intercept)の差分です。従ってATEは、
\(ATE = \lim_{w\rightarrow{0}} E [Y| t={T + w}] - \lim_{w\rightarrow{0}} E [Y| t={T - w}] \)
\( = b_1 - Y(T) \)
\( = b_1 - (b_0 + a_0 * T + \epsilon) \)
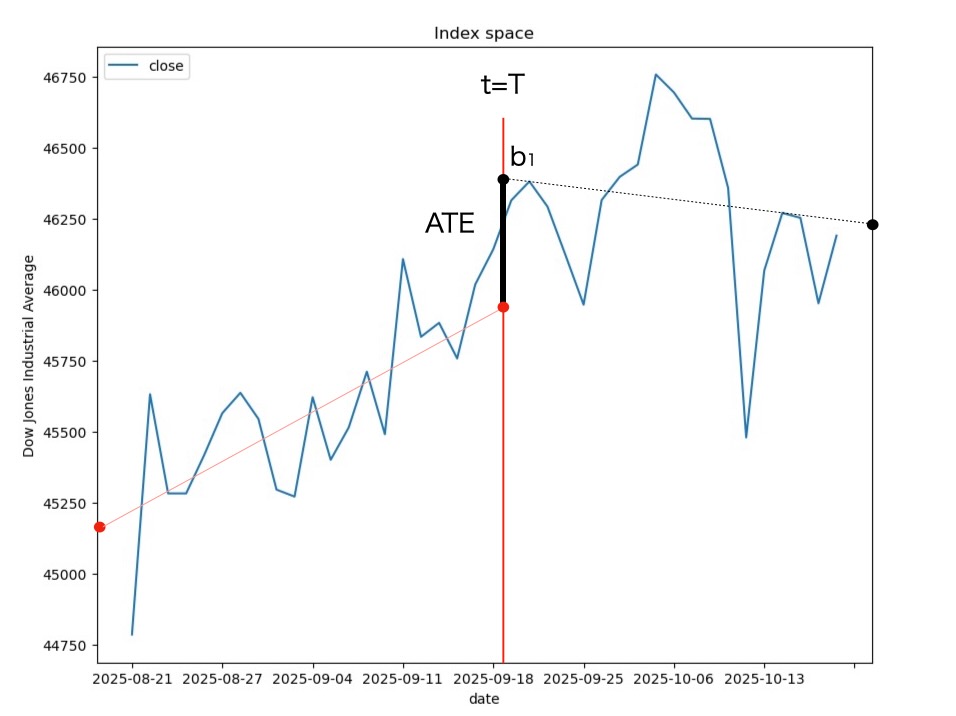
図18 イベント発生時間T前後の線形回帰、切片の差分
回帰係数の計算結果
テーブル5 DJI 9/18 ウィンドウサイズ:20
| 期間 | 処置変数 | 切片 | 傾き | Y(t = T) |
| t < T | D = 0 | 45197.6859 | 37.3786 | 45945.2472 |
| t > T | D = 1 | 46354.5197 | -7.9184 |
ATE = 46354.5197 - 45945.2472
= 409.2725
テーブル6 SP500 9/18 ウィンドウサイズ:20
| 期間 | 処置変数 | 切片 | 傾き | Y(t = T) |
| t < T | D = 0 | 6403.4050 | 10.2021 | 6607.4482 |
| t > T | D = 1 | 6670.5906 | 0.0732 |
ATE = 6670.5906 - 6607.4482
= 63.1424
次の金融政策決定会合で目標金利が変更が実施された場合、以下の形式で期待価格を予測します。信頼度と反応度を考慮して損益予測します。
\(P_t = a P_{t-1} + \epsilon \)
線形回帰モデルを株価の損益予測に使いましたが、異なる種類の資産であるT-BondはFFレートに敏感であるため、株価とは異なる結果になります。
また投資ポートフォリオの構成銘柄によって、イベントに対する反応度は異なります。
注意点として線形回帰を予測に利用する場合も期間のウィンドウサイズで結果が左右される面があります。適時、信頼度を考慮して予測に用います。
ここに取り上げた方法以外に機械学習の手法を用いた因果の影響を推定する方法があります。こちらは非線形な動作の予測にも適合できますが、株価の挙動は周期性が乏しいためヒストリカルデータの学習では、過学習になりがちです。この方法は別の機会に取り上げましょう。
備考:量的緩和の謎
以下のブログポスト"投資ポートフォリオのストレス・テスト"で触れたテーマです。非伝統的金融政策として実施された大規模量的緩和に、物価を上昇させる効果はありません。
この政策はマネタリストが支持する古典派の交換方程式に依拠しています。
\[ MV = yP \]
\[M:貨幣供給、V:流通速度、y:生産量、P:物価\]
左辺が支出側、右辺が生産側です。
日本では、物価を上昇させることを目的に、異次元緩和と称して、交換方程式の左辺にあるマネーサプライを膨張させる政策が取られました。
経済学の古典派やマネタリストの解釈では、VやYが硬直的であるため貨幣供給Mの変化が物価pに比例的な変化をもたらすとみなされています。
この解釈の何が問題かというと、統計的な比較のみで因果律を無視していることです。そのため、マネタリストの交換方程式の解釈は論理的に誤っています。
本稿ではDAGを用いた因果推論の方法を示しました。以下の簡単な例を参照してください。
C,εは正規分布に従うものとします。
\[G:= C + \epsilon \]
:= の記号は関係性を示したものです。代入を意味しています。一旦、Cの値を与えるとGが計算できます。しかしGの値を変化させてもCの値は変化しません。
この関係性には簡単なグラフ C→Gの因果関係があります。
社会的経済的なコンテキストで例えると、国が補正予算を組んで公共投資を実施するとGDPは増加しますが、マネタリーベースは増加しません。GDP→M の方向への因果の影響はありません。
交換方程式1は統計的な関係であって、左辺と右辺に相互の因果関係はないのです。マネタリーベースの増加に物価上昇に対する直接の因果の影響はありません。
異次元緩和と称した日本の大規模量的緩和政策は、実施当初から論理的に誤っていました。その誤りは10年以上に渡って継続されました。
金融政策や経済政策には、たとえその教義が論理的に誤っていても、政策を提言する人々の信仰に依拠する側面があります。
投資ポートフォリオの損益予測やリスク管理においては、こうした側面を考慮に入れておく必要があるでしょう。
- さらに、マネタリストの解釈は線形バイアスに囚われています。線形バイアスは認知バイアスの一種で、事態が定常状態であるか、または一定の割合で連続して変化していくと信じる傾向があることを示しています。 ↩︎