地政学的リスク 原油価格とインフレーション
天然資源、特に原油価格を主要因に置いたインフレーションとポートフォリオを構成する各資産のストレス・テストのシナリオの一例を図示しています。ストレス・テストとして該当シナリオ1によるポートフォリオの損益を推定します。
図１ 原油価格と地政学的リスクのシナリオ
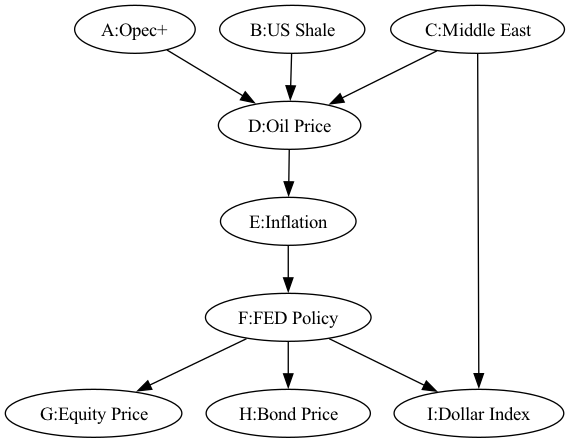
中東の紛争による地政学的リスクの上昇、原油価格の変動は、必ずしも資産価格の下落に繋がりません。これは、資産価格に影響するまでに複数の経路があることが影響しています。
リスク・シナリオをDAG(Directed Acyclic Graph)を使ったベイジアン・ネットワークで記述すると、各要因を整理し、機械学習の手法を使ってシミュレーションすることができます。
DAGで記述すると、PearlのDo操作によって、各経路のノードに固定の値を設定し、Counterfactual推論2を試みることができます。
このリスク・シナリオでは、ドル・インデックスの変動（ノード：I）に対して、地政学的リスク(中東の紛争、ノード:C）の直接の因果の経路とFEDの政策(ノード：F）を経由した経路があります。間接的な経路はバックドア経路と呼ばれ、同時確率(joint probability) P( I | F,C)で結果が逆転する現象が発生します。
次の項で簡略化した例で示しましょう。
pgmpy:因果推論のためのツールのセットアップ
以下のコラムで R に実装されたbnlearn, pcalgというDAGを基にしたベイジアン・ネットワークを使った因果探索、推論ツールを評価しました。
pythonにもDAGを記述し、条件確率テーブルを定義できるツールがあります。pgmpy3です。
これを使って、因果関係において結果に対して複数の経路を持つ同時確率（joint probability）の値の逆転する現象を示します。(シンプソンのパラドックス)
DAGとシンプソンのパラドックスは以下のコラムでも紹介しています。
ここでは、pgmpyを使って、条件確率分布から因果推論でシンプソンのパラドックスが発生する例を示します。
pgmpyをpythonの(base)環境にインストールします。最新バージョンは1.0.0です。
conda install -c conda-forge pgmpypipで環境を作っている場合は、
pip install pgmpy==1.0.0因果推論シンプソンのパラドックス
pgmpyのライブラリを読み込みます
from pgmpy.models import DiscreteBayesianNetwork
from pgmpy.inference import VariableElimination
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import CausalInference次にDAGの構造を定義します。
simp_model = DiscreteBayesianNetwork([("X", "Z"), ("Z", "Y"), ("X", "Y")])
simp_model.to_daft(node_pos={"Z": (0, 0), "Y": (2, 0), "X": (1, 1)}).render()
条件確率テーブルを定義します。
cpd_x = TabularCPD(
variable="X", variable_card=2, values=[[0.5], [0.5]], state_names={"X": ["a", "b"]}
)
cpd_z = TabularCPD(
variable="Z",
variable_card=2,
values=[[0.25, 0.75], [0.75, 0.25]],
evidence=["X"],
evidence_card=[2],
state_names={"X": ["a", "b"], "Z": [0, 1]},
)
cpd_y = TabularCPD(
variable="Y",
variable_card=2,
values=[[0.3, 0.4, 0.7, 0.8], [0.7, 0.6, 0.3, 0.2]],
evidence=["X", "Z"],
evidence_card=[2, 2],
state_names={"X": ["a", "b"], "Z": [0, 1], "Y": [0, 1]},
)
simp_model.add_cpds(cpd_x, cpd_z, cpd_y)条件確率分布を求めるのに、pgmpyは複数のアルゴリズムを提供しています。VariableEliminationは確率的な推論です。Counterfactual推論：与えられた条件でモデルを調整します。Tの観測条件による推論。
infer_non_adjust = VariableElimination(simp_model)
print(infer_non_adjust.query(variables=["C"], evidence={"T": 1}))
print(infer_non_adjust.query(variables=["C"], evidence={"T": 0}))+------+----------+
| Y | phi(Y) |
+======+==========+
| Y(0) | 0.5000 |
+------+----------+
| Y(1) | 0.5000 |
+------+----------+
+------+----------+
| Y | phi(Y) |
+======+==========+
| Y(0) | 0.6000 |
+------+----------+
| Y(1) | 0.4000 |
+------+----------+ CausalInferenceは、与えられた結果と影響により、因果関係を推定する特徴を与えます。
以下はdo-操作による因果推論です。
infer_adjusted = CausalInference(simp_model)
print(infer_adjusted.query(variables=["C"], do={"T": 1}))
print(infer_adjusted.query(variables=["C"], do={"T": 0}))Loading widget...
+------+----------+
| Y | phi(Y) |
+======+==========+
| Y(0) | 0.6000 |
+------+----------+
| Y(1) | 0.4000 |
+------+----------+
Error displaying widget
+------+----------+
| Y | phi(Y) |
+======+==========+
| Y(0) | 0.5000 |
+------+----------+
| Y(1) | 0.5000 |
+------+----------+二つの条件確率テーブルを示しました。
推論によって、結果の値が逆転しているのを示しています。
関数VariableEliminationは、同時確率で、影響のない変数を排除します。
query()は、条件確率 P(Y | X=1) と P(Y | X=0)の値を出力します。
バックドア経路がある場合、原因となる値(X)に依存して、結果(Y)が逆転することが示せます。
システミック・リスク、金融による景気刺激策
複雑な社会現象は相互に関連しあっており、DAGで現象を記述すると多くの潜在的な要因を経由した因果の経路の存在を示すことができます。
量的緩和パズル
以下の図２は、金融政策の景気への影響を貸出や投資という銀行の役割に注目して因果関係を示したものです。
図２ 金融緩和のDAG
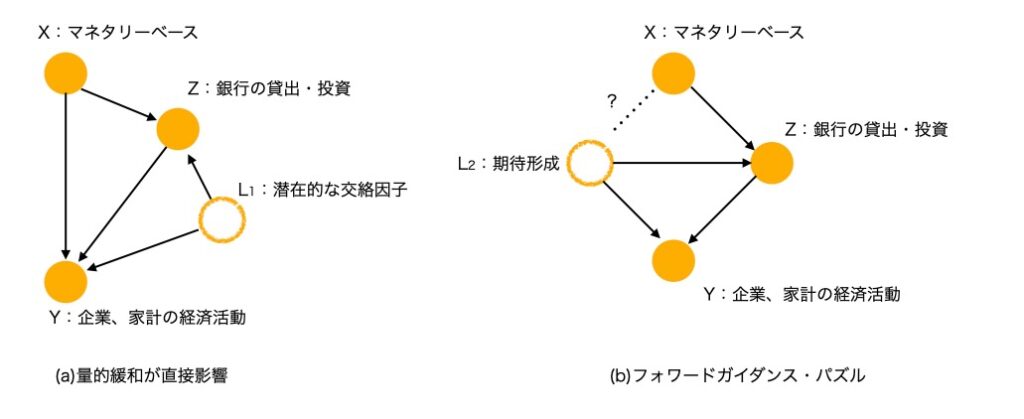
図のLは潜在的な交絡因子です。アニマルスピリットのような、有利子負債を増やして設備投資を拡大させる傾向の強さなどを潜在変数として定義しています。DAGで示したように、X -> Yに直接、因果の経路と間接的な経路のあるこの種のDAGでは、前項で示したシンプソンのパラドックスが発生します。つまり、条件に依存して効果が逆転する現象が起きるのです。
これは、以下のコラムで紹介したニューケインジアンのリバーサル・レイトという考え方と整合性が取れます。
量的緩和、大規模な緩和策を実行する根拠は、古典派の貨幣数量説に依拠しています。
以下の数式で示す交換方程式という線形的な関係です。
MV = yP ーーーーーー（*１）M:貨幣供給、V:流通速度、y:産出量、P:物価
経済学では、こうした線形的な関係が前提にされます。
図２では、ノードX:M, ノードY: yPに擬似的に対応させることができます。図３(b)は、X->Yへの直接の因果の経路はありませんが、金融緩和へのコミットメントが期待形成に働きかけるという経路を点線と?印で示しています。上のコラム３でも解説していますが、これはフォワードガイダンス・パズルとして、期待形成に働きかける経路は疑わしいことが検証結果に示されています。(注）
（注）
Marco Del Negro, Marc Giannoni, Christina Patterson,. Th Foward Guidance Puzzle; Federal Reserve Bank of New York Staff Reportd. October 2012, Revised December 2015.
上記、(*1)の等式は、本来、左辺と右辺の相関関係を示すものであり、因果関係を示すものとしては定義されていません。Mの増加が総生産(yP)を駆動することを意味していません。図３(a)のXY間のエッジの方向が正しいとは断定できません。
古典派の解釈では、yやVが硬直的であるため、貨幣供給Mの増加が物価Pに比例的な変化をもたらすとみなされていました。この交換方程式が示す相関関係があるとしても、現代ではクレジット決済やキャッシュレス決済、電子決済でVが上がっており、貨幣Mの取引需要はそれほど必要とされない側面もあります。
以下のコラム４のIS-LM分析でも示しましたが、ある条件下では、マネーサプライの増加が利子率の低下を通じて総生産を増加させることはあります。低金利下では、マネーサプライの増減が、総生産に影響を与える原因にはなりません。むしろ、過大な金融緩和が景気に対して逆の効果をもたらす（上記コラム３）場合もあるのです。
貨幣数量説のように簡略化した線形に等式が成立するのは、非常に狭い特定の条件の時だけです。いくつかの錯誤に基づく仮定の上で、日本の異次元緩和と称される緩和策は実行されました。政治家は経済政策によって燃え盛るような景気を期待するものです。
ここで繰り返し例を示したように、マクロな社会現象であるインフレーションとマネタリーベースの増加に線形的な関係を普遍的に適用することはできません。
規模を拡大しても、それに比例した大きさの効果が得られません。両者の因果関係を単純な線形関係で記述できないためです。多くのバックドア経路や潜在変数が存在しているとみなす方が現実的です。
図３(b)の因果構造モデルでは、M(MV)に該当するマネタリーベース：ノードXと、yPに該当する経済活動：ノードYは、期待形成という条件に関して独立した変数になります。[ P (Y ⊥ X | Z) ]
DAGはベイジアン・ネットワークで確率的な因果関係を示します。こうした確率的な関係は、現実社会に現象の因果関係をうまく記述できます。
下の図４を参照してください。ベイジアン・ネットワークはDAGのノード間を結ぶ矢印が直接、因果関係を示しています。
図４ 相関関係 ≠ 因果関係
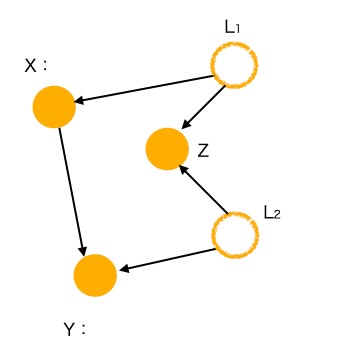
図４のノード：Z、Yに因果関係はありません。(Zの変化は直接Yに影響しません）が、両者に共通する原因(L2)に起因して相関関係は発生します。
経済学では、合成の誤謬と表現される現象が知られています。個々の正しい選択が、全体で誤った結果を発生させます。
数学、統計では、前項でみてきたように同時確率(joint probabity)で逆転が発生することがあります（シンプソンのパラドックス）。
このパラドックスは統計の分野では、古くから知られたありふれて発生する現象です。この現象は前項で例示したように、DAGを用いて正確に記述できることが知られています。
合成の誤謬は社会現象ではありふれて発生し、DAGを使って、同時確率(joint probability)の逆転として正確に記述することができます。
図２(a)は、(*1)の等式で示す貨幣数量説にも適応した因果の構造を示すベイジアン・ネットワークの例です。因果の経路として、直接作用する経路(X->Y)以外に、バックドア経路と呼ばれるZを経由した経路が存在します。この種のネットワークでは、結果としての同時確率(joint probability)に逆転が発生します。図２(a)のDAGで示すバックドア経路のあるネットワークは、結果の解釈が潜在的に逆転する構造があり、各ノードの変数間に単調な線形的な関係は必ずしも成立しません。
図２で示す因果の構造の中では、貨幣数量説による正の相関は成立しないのです。この変数の相関関係はある特定の条件の時のみ成立します。大規模化しても、結果が線形的に影響され、効果が大きくなるわけではありません。
あまりにも低すぎる金利でのさらなる金融緩和は銀行の収益率を減らし、信用供与を減少させます。低金利の期間が長期にわたる場合も同様です。
統計処理では、逆転現象に遭遇した場合、観測データ自体では逆転の理由が判別できないため、上の参照しているコラム２で解説しているような、逆転する現象に対する背景知識が必要になります。
マネタリーベースを誇大化させた日本の金融緩和政策は、忖度を基に実行されたためか、過度の緩和が継続され、日銀のバランスシートは歪になりました。
他の国でも金融政策を担当する中央銀行の独立性が担保されない例は散見されます。
懸念すべきこととして、現在のインフレーションが量的緩和の効果だとみなす誤解が広く信じられています。この誤認により間違った処置が実施される傾向があります。今後、大規模金融緩和によってインフレーションになったという錯誤を前提に、経済政策が実行されかねません。これはシステミック・リスクの一つです。あたかも経済政策とみなされている外国為替市場介入も同様のリスクの一つです。
ここで述べた因果関係を示すDAGを使ったベイジアン・ネットワークは、事象の因果の構造を正確に示し、事象間の関係を確率的に記述することができます。
国内外の経済政策のシステミック・リスクに関して、ポートフォリオのストレス・テストを実施するのに、DAGを基にシナリオをモデル化しシミュレーションします。どのような政策も、Counterfactualという手法で想定した仮想的な状況をシミュレートすることができます。
因果推論やモデル化において、ここで使用したpgmpy以外にもRによるpcalg, bnlearnなど、ベイジアン・ネットワークに関する多数のツールが利用できるようになりました。以下の表は、ここに挙げたパッケージが実装している機能を示しています。
| パッケージ | 構造の学習 | パラメータの学習 | 推論 | シミュレーション | 因果推論 | 因果のシミュレーション | モデルテスト |
| pgmpy | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| bnlearn | ○ | ○ | ○ | ○ | |||
| pcalg | ○ | ○ | ○ | ○ | ○ |
構造の学習は以下のアルゴリズムを含みます。
- PC
- Hil-Climb Search
- Max-min Hill-Climbing
パラメータの学習は以下のアルゴリズムを含みます。
- Maximum Likelihood
- Bayesian Estimator
- Expectation Maximization
参考資料
- Marco Del Negro, Marc Giannoni, Christina Patterson,. Th Foward Guidance Puzzle; Federal Reserve Bank of New York Staff Reportd. October 2012, Revised December 2015.
- Judea Pearl, Causality: Models, Reasoning, and Inference.
- Judea Pearl , Dana Mackenzie, The Book of Why, The new Science of Cause and Effect.
- Ankur Ankan, Johannes Textor. pgmpy: A Python Toolkit for Bayesian Networks,
