経済や金融の分野で、統計的な手法を使って市場を分析していると、実際の経済現象と一般に認識されている経済状況の間でパラドックスに出会うことがあります。
大規模金融緩和や長期間の金融緩和が経済活動の縮小を招くことや、通貨当局の外国為替市場介入により当局の意図とは逆方向に為替レートが推移することなどは、このサイトでも紹介しています。
ここでは以前、データの因果性を解析するツールの一つとしてcausal-learnや、CausalPyを紹介しました。パラドックスのように映る経済現象を正しく認知する上で因果性が重要なためです。
本稿では、これらを一般化して、なぜ因果性が統計的な思考より、本質的な問題の解答と分析のために必要なのかを解説します。統計的な方法の限界を示すために、シンプソンのパラドックスを例に取ります。
シンプソンのパラドックス
シンプソンのパラドックスは統計の分野ではよく引用されるパラドックスです。Edward H. Simpsonによって1951年に技術的な論文として発表されました。これは変数X,Yの対の間の関係が、第3の変数Zの条件によって、そのZの値に関わらず、逆の符号となる現象として知られます。
LindleyとNovick(1981)によって”因果関係の言語”でパラドックスを説明することが可能だと言及されましたが、うまく定義されていませんでした。シンプソンの論文には、”因果”の用語は出てきません。シンプソン自身の表現では、それはデータの背後にあるストーリーに依存しており、より”注意深い解釈”が一塊のデータと、部分的なデータの間で互換性を持つことがあると表現しています。
この例を下の図1に示します。Wikiの図が分かりやすいので、図1にリンクを貼っています。
Correlation
図1 シンプソンのパラドックス Wikiより参照
二つの変数間で負の関係が見られる中で、データが多重グループが結合したものだった場合に、その関係が消えるだけでなく逆の関係を示します。
この逆転は、危機的な意思決定の状況で難しい選択に導くかもしれません。
他にも、統計の分野で類似の現象として抑制効果(Suppression effect)、ロードのパラドックス(Frederic M. Lord in 1967)が知られています。これら三つの統計的なパラドックスは、同じ性質を共有します:二つの変数間の関係が、他のもう一つの変数が統計的に操作されるときに、逆転、減少、または拡張されます。抑制効果、シンプソンのパラドックス、ロードのパラドックスは全て同じ現象で、逆転するパラドックス(reversal paradox)です。
以下に例を示します。シンプソンのパラドックスのテスト用に擬似的にデータセットを生成し、線形回帰を使って統計的に処理します。
シミュレーションによる線形回帰モデル
最初にモデルを定義し、テストデータセットとしてランダム変数を生成します。モデルは予め、五つのグループを設定し、グループ毎にランダムデータを生成します。以下に生成したデータを表示します。
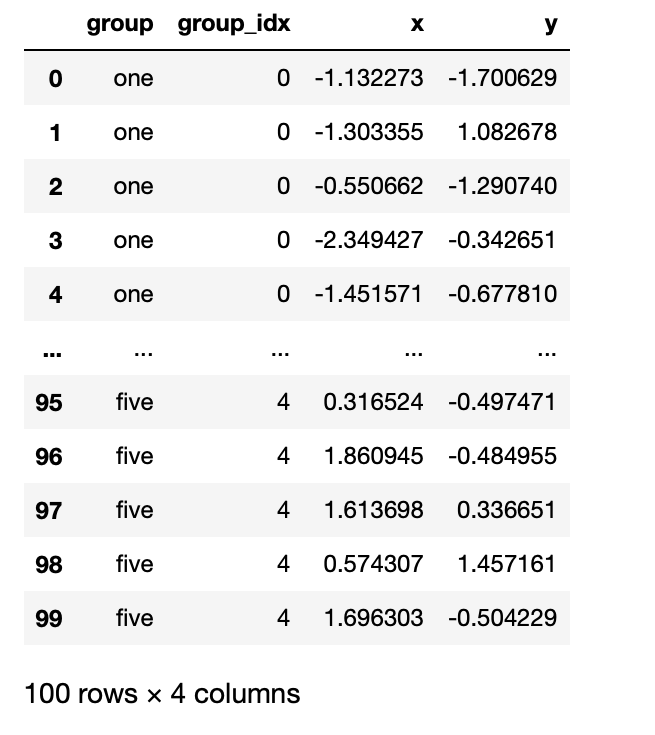
図2 生成したデータセット
データセットをプロットします。
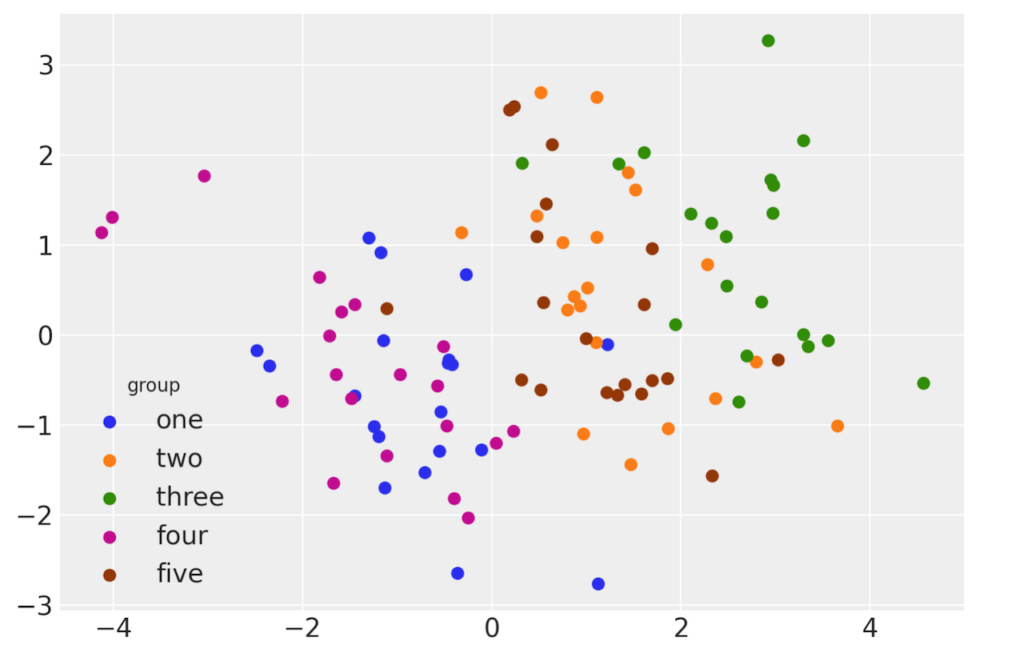
図3 生成したデータセットのプロット
データ全体を一塊に扱った場合の線形回帰です。XとYは正の相関を持っています。
これはモデルに関する知識がない場合です。
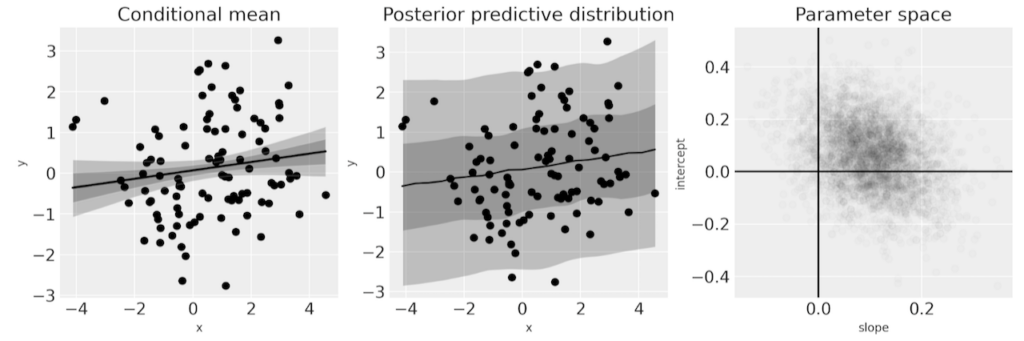
図4 一塊のデータの線形回帰
次にグループレベルでモデル化した場合の回帰分析です。データがグループになっているという知識を使います。
データのグループ情報を元にして、グループ毎に線形回帰1を実施します。
図5はパラメータをモンテカルロシミュレーションでサンプリングした結果です。
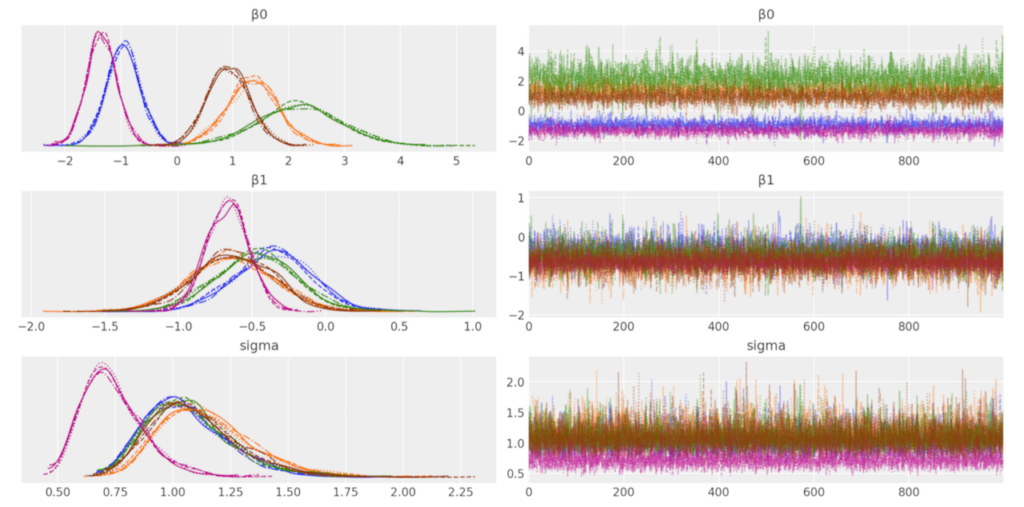
図5 サンプリングしたパラメータ
グループレベルの線形回帰の例です。
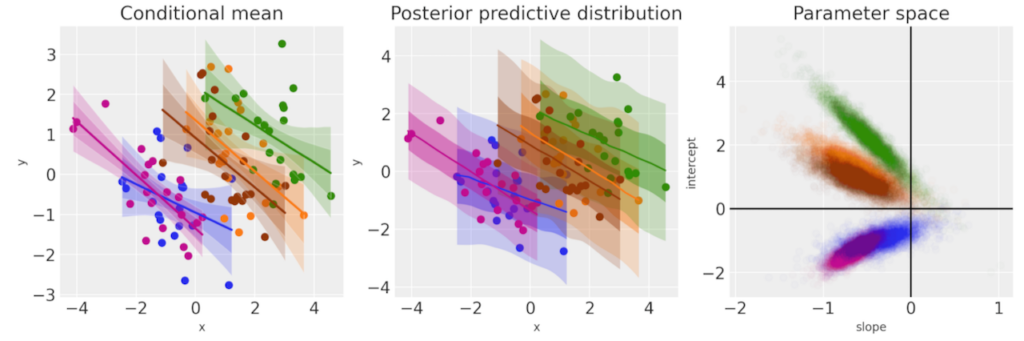
図6 グループレベルの線形回帰
グループレベルでモデル化した場合は、変数XとYの間に負の関係があることがわかります。
このグループレベルのデータに対する回帰の傾きが負であることから、これは図4の結果と矛盾したもの(パラドックス)になります。
シンプソンのパラドックスが示された論文には因果の概念は示されていません。統計的な処理として二つの内容が、私たちに同じデータを元にした二つの反対の行動を引き起こさせる場合に、私たちの決定は統計的な考えによらないだけでなく、その内容から抽出される何らかの付加的な情報によって決定される必要があります。
正しい解答は、まとまっていないデータの中に置かれた一つの正しい答えより、全体では異なる因果関係を持っているまとまったデータの中にあることを示します。
上の図4と図6の二つの例では、付加的な情報がなければ、どちらが正しいデータかわかりません。
2番目の関係は、データがある基準によってグループになっているという知識を追加すると、グループレベルでモデル化した回帰分析が正しいことがわかります。
具体例として、解熱剤のような薬の効果について考えてみてください。Y軸が体温の変化だとすると、データ全体を一塊に扱った場合、薬の処方の効果はなく、むしろ逆相関のために処方によって症状が悪化(発熱)していることを示しています。
しかし、グループ情報があると、処方の効果があることがわかります。このグループが第3の変数として年齢のような世代間の情報を元にグループ化されている場合です。同世代でみた場合に処方に効果があることがわかります。
どのような薬も、最初の段階で、年齢や性別に効果の相違があることはわからないため、パラドックスが発生します。
因果の構造
因果性は、これに変革をもたらしました。因果の構造はシンプソンの逆転をサポートすることがわかっているだけでなく、どの構造が全てのデータ、またはまとまっていないデータに関して正しい答えをもたらすかもわかります。
さらに、正しい答えが置かれている予測のための基準は、第3の変数が処置によって影響されるかどうかによって決まるのでなく、むしろ一時的な情報に鈍感であることがわかっています。
変数は因果のダイアグラムの中で経路をトレースする”バックドア”と呼ばれる簡単なグラフィカルな条件を含みます。そして、処置から結果までのすべての見せかけの経路は、第3の変数によって区切られることが保障されます。
ソリューションは以下を満たすものです。
- なぜ人々が現象に驚かされるか、または信じられないと考えるか説明する必要があります。
- パラドックスが直面する、そしてそれから区別するシナリオのクラスを識別する必要があります。
- 最後にパラドックスが優柔不断に導くそれらのシナリオの中で、正しい解答を識別する必要があり、その選択に導くシナリオの特徴を説明する必要があります。
この因果性はシナリオのクラスで識別し、記述することが可能であることが必要です。
シナリオの期間は、データを生成する過程を含むので、連続する矢印で操作するどのようなデータ生成過程もシミュレートできるものとします。そうした過程の適切な言語は、因果ダイアグラムです。
与えられたシナリオの科学的な内容は、DAG(Directed Acyclic Graph)の様式に符号化することができます。データ生成過程は、与えられたシナリオと互換性を持ちます。
グラフィカルモデルの理論は、与えられたDAGにとって、シンプソンの逆転が実現されるか、または論理的に不可能であるかどうかを教えてくれます。
以下のような因果の構造でシンプソンの逆転が発生します。
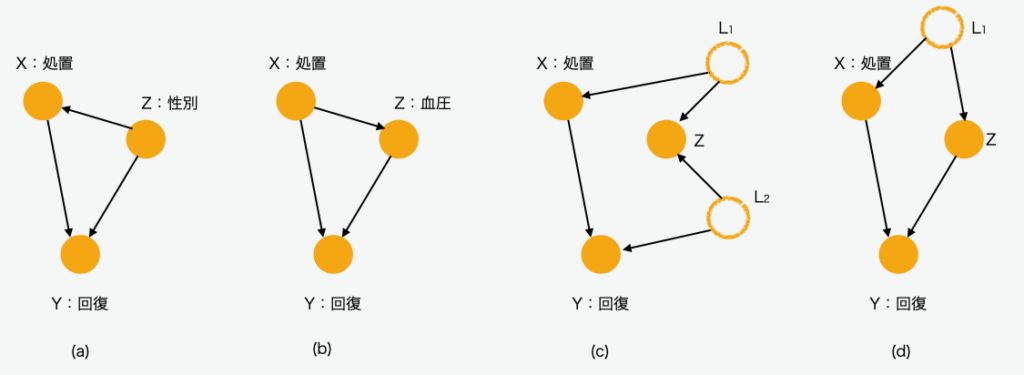
図7 シンプソンの逆転が発生する因果の構造
図7に挙げたDAGはシンプソンの逆転が発生します。L1、L2の記号は、観測されない潜在変数(latent variable)を意味します。
このDAGは時系列な情報が十分ではありません。モデルの(c)と(d)は処置Xを施す前か、あるいは後で発生するかもしれません。このタイミングでは正しい答えはまだ不定です。モデル(c)ではZは条件にならず、モデル(d)では条件にすべきです。両モデルとも処置XによってZの値は影響されません。
図7(c)を見ると、相関関係と因果関係が明確に区別されることがわかります。Yと第3の変数Zは潜在変数のL2の影響を受けることで相関することはありますが、変数Zの変化がYに影響することはありません。Zの条件はYの値に影響せず、因果関係はありません。しかし、結果として相関関係を持つことがあります。
パラドックス解決のためには、逆転が発生するときに、正しい判断を下すことができることをはっきりと立証します。これは、シミュレーションによるか、または数学的に達成することができます。数学的には、do-calculus2という代数学的な方法を使います。do-calculusは、私たちがグラフィカルな基準を使っていることの正しさを証明することになります。
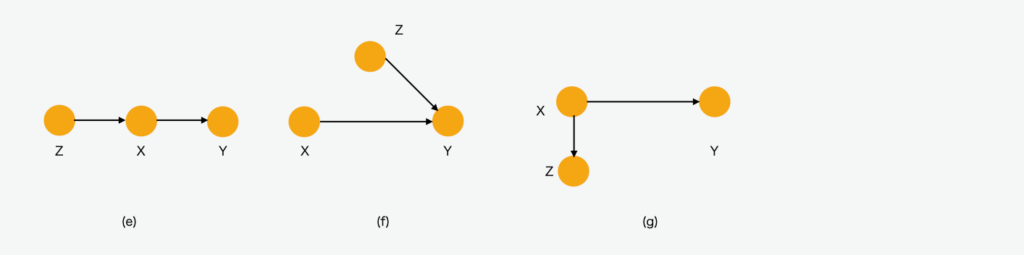
図8 因果の構造2
図8(e),(f),(g)で示すDAGでは、逆転のパラドックスは発生しません。
これは、どのようにバックドア基準が働くか、どこに正しい答えがあるか説明します。原理は簡潔です:XとYを接続する経路は、因果性と見せかけの関係性の2種類あります。因果性のある関係は、XからYへ直接矢印が接続されます。他の経路は見せかけの関連性を伝達し、適当な共変量(covariate)のセットの条件によってブロックされる必要があります。Xの中に矢印を向けるすべての経路は、見せかけの経路で、選択された共変量のセットで区切られる必要があります。
シンプソンのパラドックスと関連現象は、非経験的なデータの因果分析上の適合性と共変量の選択の問題です。因果分析を導くために、統計的な基準を使うことで(生命を脅かすような)危険に晒しますが、その統計的な基準がそれらを表現する現象の説明を保持していないばかりか、それを避ける方法も示していないということを強調しなければなりません。
その理由の説明とソリューションは、統計的な基準でなく背景知識(background knowledge)に依拠した、因果分析に存在しています。
ドル円為替レートへの外国為替市場介入
為替レートの推移(Y)と通貨当局による市場介入(X)に対する構造化因果モデルのDAGは以下の図9で示すように定義できます。
市場介入が直面するパラドックスのシナリオには、政府の市場介入と結果としての為替レートの間に、詐欺グループによる裁定取引のフラウドリスク要因がリスク因子、第3の変数Zとして介在します。
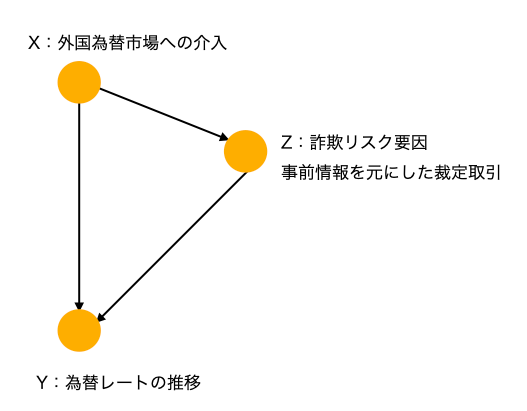
図9 外国為替市場介入と為替レートのDAG
このDAGでは、市場介入の結果、介入資金が詐欺グループに供与され、詐欺グループの投機によって、為替レートは介入意図とは逆方向に推移します。外国為替市場介入のパラドックスは、DAGで記述すると、その影響と効果を識別することが容易になります。
図7(b)のケースと同様に、市場介入によって裁定取引が実施され、介入資金がその取引の決済資金となるため、流動性が厚くなり為替レートがシフトしないだけでなく、供与した資金によって、さらに介入資金を騙取するための当局の意図とは逆方向への取引が進みます。
この変数Zは、為替レートの狭い範囲における流動性の上昇として観測できます。(例えば、USD JPYレートの連続した値幅0.1円における取引量の変化)
日本の外国為替市場介入は、2002年以後、ほぼ確実に(すべての介入機会が)詐欺グループの裁定取引の対象になるため、為替レートを意図した方向に推移させることはできません。外国為替平衡操作の実際の効果は、為替レートとは無関係に国の予算の特別会計から詐欺グループへ資金供与しているだけです。
どのような立場の人間もバイアスを持ちます。これは認知におけるH.A. サイモンのハサミのアナロジーが示す、合理性の限界です。市場介入の事前情報を利用した内通者による取引という経済現象の背景にある環境が認知されない、あるいは意図的に隠蔽されるために、市場介入に効果がなくても同じ操作を試み、詐欺グループに資金を供与し続けることになります。
参考資料
- Judea Pearl , Comment:Understanding Simpson’s Paradox.
- Onyebuchi A Arah, The role of causal reasoning in understanding Simpson’s paradox, Load’s paradox, and the suppression effect: covariate selection in the analysis of observational studies.
- Judea Pearl & Dana Mackenzie, The Book of Why, The New Science of Cause and Effect.
- Judea Pearl, Causality: Models, Reasoning, and Inference. (2nd ed.).
μ = β0 + β1 * x
y は正規分布に従うものとします。 ↩︎- do-operator :do(X)は物理的な干渉(intervention)を意味します。モデルの他の部分は変化させずに変数Xを強制的に定数X=xで置き換えます。do(x)と(X)の違いは、干渉(doing)と参照(seeing)の相違です。"因果推論"は、純粋に観測(seeing)されたデータを元にして、干渉(doing)の結果を推論することを試みることとみなすことができます。
do-Calculusには三つのルールがあります。
【ルール1】 観測(Observations)の挿入/削除
変数X ,W,ZとYの関係で変数Wは観測できますが、Yとは無関係である時にYの確率分布は変わりません。この時この関係性は以下のように変換できます。
P(Y |do(X),Z,W) = P(Y |do(X),Z)条件確率から変数Wの影響は無くなります。
【ルール2】 干渉(Action)/観測(Observation)の交換
バックドアの経路を考えると、変数ZのセットがXからYへのすべてのバックドアの経路をブロックされ、Zだけが条件になるとdo(X)は(X)の参照と等価になります。
P(Y |do(X),Z) = P(Y |X,Z)Zがバックドア基準を満足する場合
【ルール3】 干渉(Actions)の挿入/削除
確率式から干渉do()を削除、追加します。Yに対するdo(Z)の影響が無くなる状況です。
P(Y |do(X),do(Z),W) = P(Y |do(X),W)(Y とZが独立|X,Wの条件で)
do-Calculusのより詳しい内容は、参考資料(4)の3章に記載されています。 ↩︎